Noesis
The Journal of the Mega Society
Number 133
July 1997
EDITORIAL
Chris Cole
P O Box 10119
Newport Beach, CA 92658
An important ballot is included in this issue. Please tear it out, vote, and send it in.
CONTENTS
THE 10-MARBLES PROBLEM by Chris Cole
HIGH RANGE TESTS by Chris Cole
BALLOT (center page)
LETTERS on the 3 CUBES PROBLEM by Ronald Penner
THE 10-MARBLES PROBLEM
Chris Cole
Chris Langan argues:
For example, suppose that the method of filling the box was chosen deliberately to conceal the nature of the prior distribution. E.g., suppose that the prior distribution consisted of 10 white and 10 million nonwhite marbles of various specific colors, but that the 10 white marbles were deliberately sought out and put in the box. Then virtually all continuity between the prior distribution and the subsequent observations has been destroyed, and knowledge of the prior distribution – in which nonwhite marbles were a million times more numerous than the white ones – can only interfere with accuracy. Since we cannot assume that the contents of the box reflect the prior distribution, knowledge of the prior distribution cannot be necessary.
In this paragraph, Chris appears to misunderstand the term “prior distribution.” The prior distribution is the distribution of the colors of the marbles produced by whatever selection rule is used to fill the box, not the distribution of the marbles in whatever pool they were selected from. Thus, if only white marbles are selected, the prior distribution is 100% white; if a coin was flipped, you get a binomial distribution, etc.
Chris also argues:
This brings up a very basic distinction between logic and probability, or deterministic and probabilistic reasoning. Probability does not have to be perfect; it only has to be valid in “most cases.” Unlike deterministic constraint, which can be factually invalidated by counterexample, probability is invulnerable to occasional bursts of improbable short-term data. Such deviations are inevitable, and we cannot require probabilistic theorems to forecast every one of them specifically.
Here, Chris appears to misunderstand the term “probability.” The theory of probability is derivable from set theory; it is a branch of mathematics; it is no more or less perfect than logic. Statements of probability always are uncertain to some degree, because, like logic, they depend upon the assumptions that are made. This is all that Bayesian Regression has to say; it is really not that big of a deal.
Chris issues this challenge to me:
I predict that you cannot find one (1) professional probability theorist, now working for a college or university in the U.S., who will back your viewpoint … i.e., who will identify himself fully and say in print that the law of large numbers – or the relationship of frequency to probability that it implies – fails to apply to a closed and finite set of marbles in a box.
And again, Chris appears to misunderstand what the “law of large numbers” means. In a general way, this law states that error decreases as the number of samples increases. Thus, for example, after you select ten white marbles from the box it is more likely that there are only white marbles in the box than it was after you had only selected five white marbles from the box. But the law of large numbers certainly does not say that the odds are precisely .67. As for his challenge, I’ll do Chris one better: I’ll randomly select a probability theorist and send the problem to him.
But before we waste the effort, maybe this will help. Instead of talking about white and nonwhite marbles, let’s talk about boy and girl children. Are you saying, Chris, that if I sample (with replacement) ten children from a family of ten, and all of them are girls, then the odds are .67 that they are all girls? No? How about if I sample them from a classroom? Still no? How about if I sample them from a parking lot? Maybe? How about from the beauty salon? Yes? Why the different answers in different cases? Could it be because you have different estimates of the prior distributions in each case?
HIGH RANGE TESTS
Chris Cole
Chris Langan argues:
You [me] made the following two statements. “It is enough for me to know that the authors of the tests (taken by Paul Maxim) do not claim that they can be used to distinguish at the one-in-a-million level. I think we should believe them.” In the interest of fairness, let me add the following equally valid statements. “It is enough for me to know that he authors of the tests (taken by Paul Maxim) do not claim that they cannot be used to distinguish at the one-in-a-million level. I think we should believe them.” See? Now things are back in balance. Tests like the Pintner may be “low range” in comparison to tests like the Mega, but their ranges are more than adequate for a sufficiently young (mega-level) child.
In issue 126, I stated that I would not spend time discussing the concept of “range” in testing because I felt the members already understood it. From the above it is clear that at least one member does not. First of all, let me explain why I do not think childhood IQ scores can be used for admission to Mega. A childhood IQ score is frequently computed using “mental age” divided by “physical age,” so that a person scoring 200 at the age of ten has done as well on the test as an average person of twenty. However, we also hear that IQ as measured by several popular tests has a mean of 100 and a standard deviation of 16. How can these both be true? The answer is that near the mean (100) the population is roughly normally distributed, with a standard deviation of 16. Out near the Mega level, the distribution looks nothing like the tail of a bell curve, and we certainly cannot conclude that someone scoring 176 on a childhood IQ test is at the one-in-a-million level.
Secondly, the designers of IQ tests are trying to find out where people are near the mean; they are not trying to explore the Mega level. Cynics would point out that this is because there is no market up there. I’m sure that is part of the story, but in addition we should recognize that many of these tests are intended to diagnose learning disabilities, so that, if they deviate from the mean at all, they concentrate on the low side. The purpose of the tests is to distinguish people who are near or below the mean. A test designed to do this must be composed of relatively easy problems. To see why, I have run a simulation. I created three different “tests” – one easy, one medium, one hard. The easy test is composed of 500 easy problems, the medium test is composed of 500 medium problems, and the hard test is composed of 500 hard problems. What is an easy, medium or hard problem? A graph explains it better than words:
Graph of Problem Difficulty
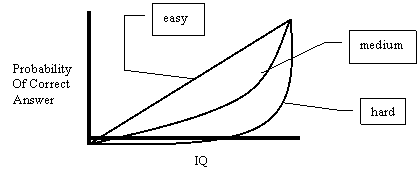 |
The histograms below show the results of the simulated taking of this test by 10,000 “people.” The people were uniformly distributed across intelligence, except two extra points were added at the high end. Intelligence is measured on an arbitrary scale from 0 to 1; a person with intelligence of 0.5 is five times more likely to correctly answer an easy problem than a person with intelligence of 0.1, for example. The asterisks on the histograms represent two standard deviations around the mean for each intelligence level. What the test designer is looking for is to make sure that the lines for 0.5, for example, do not overlap the lines for 0.4 or 0.6.
These histograms show that the easy test does a good job of spreading out the people with intelligence from 0.1 to 0.8, and a poor job above this. The hard test, on the other hand, does a poor job of distinguishing intelligence below 0.5, and better above this.
easy:
0.1 ****
0.2 ****
0.3 ******
0.4 ******
0.5 ******
0.6 ******
0.7 ******
0.8 ******
0.9 ****
0.95 ***
0.99 **
medium:
0.1 *
0.2 ***
0.3 ****
0.4 *****
0.5 *****
0.6 *****
0.7 ******
0.8 ******
0.9 *****
0.95 ****
0.99 **
hard:
0.1
0.2 *
0.3 ***
0.4 ***
0.5 *****
0.6 *****
0.7 *****
0.8 ******
0.9 *****
0.95 *****
0.99 **
Thus, we do not need to be explicitly told by the designers of the Pintner test, or any other standard intelligence test, that they are not valid in the Mega range. If they were valid in the Mega range, then they would be useless in the normal (100) range. It is simply impossible to design a test that is valid in both ranges. This has nothing to do with the number of people that took the Pintner test, how big the norming sample was, what the intended age of the testees was, etc. To claim otherwise is bad science.
MEGA SOCIETY BALLOT
Enter your name: _________________________________________________
Indicate your vote on any or all of the following proposals and mail your ballot by September 15 to:
Jeff Ward
13155 Wimberly Square #284
San Diego, CA 92128
Vote for ONLY ONE of the next three proposals. Indicate your choice in the box to the left.
1. The Bylaws of the Mega Society shall be as published in Noesis issue 123.
Enter 1, 2, or 3:
2. The Bylaws of the Mega Society shall be as published in Noesis
issue 123, amended as proposed by Kevin Langdon in Noesis issue 125.
3. The Bylaws of the Mega Society shall be:
The Mega Society shall have three positions elected by a majority vote of those members casting valid ballots: Administrator, Editor, and Publisher. The term of these positions shall be two years. The Administrator shall handle administrative matters such as elections and applications for membership. To be admitted to membership, a person must have scored at or above the one-in-a-million level on a test of general intelligence, and must pay an initiation fee of $15. The Publisher shall publish and the Editor shall edit the newsletter. Subscription fees for the newsletter shall be set to an amount sufficient to cover the cost of publication and distribution. Bylaw changes and major decisions regarding the governance of the Society shall be decided by a majority vote of those members castings valid ballots.
Vote YES or NO for the following proposals.
NO YES
Jeff Ward shall be the Administrator of the Mega Society.
NO YES
Chris Cole shall be the Publisher of the Mega Society.
NO YES
I nominate myself to be the Editor of the Mega Society.
NO YES
To be acceptable as an admission test for the Mega Society, a test must
be credibly claimed by its author(s) to be able to distinguish intelligence at
the one-in-a-million level.
NO YES
The following tests are to be used for admission to the Mega Society:
The Mega Test by Ron Hoeflin
The Titan Test by Ron Hoeflin
![]()
![]()