4-23-98
Dear Kevin,
I'm sorry to tell you this, but the formula for combining scores that Dr. Hoeflin uses in his article ``The Statistical Technique for Combining IQ Scores'' is quite correct.
You are also mistaken in believing highly g loaded tests are more highly correlated at their high end than over their full range. Actually, the exact opposite is true: reliabilities, g loadings and correlations with other tests and criteria drop at both ends of a test.
On the other hand, while Dr. Hoeflin got the formula correct, he solved the problem incorrectly. When you combine test scores you must use the metrics of the tests being used (mean and standard deviation), and not the metrics for the general population, which is what Dr. Hoeflin used.
Here's how the problem should be solved:
The tests developed for the super-high-IQ societies have averaged a mean of about 142 and a standard deviation of about 9.5 points. Some means were a little higher and some a little lower, and standard deviations were sometimes greater and sometimes smaller. Nevertheless, I regard these as good average figures.
Let's hypothesize two super-high IQ tests with these metrics that correlate .6 as Dr. Hoeflin suggests. Here's what we get:
| 176 = | ( |
(173-142)+(173-142) |
) |
9.5 + 142 |
| sqr(9.52 + 9.52 + 2(.6)(9.5)(9.5)) |
In other words, you would need two tests with scores equal to or greater than 173 to be equal to or greater than 176. Not much of a gain.
The only way to combine two super-high-IQ tests with scores of 168 or better to get 176 or better would be if the correlation between tests was zero.
As a matter of fact, this actually occurs. While the correlation between the LAIT and the Mega Test is high, the correlation with the non-verbal part is still higher. On the other hand, the LAIT's correlation with the verbal subsection of the Mega Test is effectively zero. (I get a correlation of .16, which for the sample size I used is, statistically speaking, not significantly different from zero.)
I'm surprised that you're all struggling with this problem. The answer's obvious. Combine all the super-high-IQ tests available. Other things being equal, the longer a test is the more reliable it is. The more reliable it is, the higher the g loading tends to be. The higher the g loading, the more the test will correlate with things in the real world that you want to predict.
4-27-98 (excerpt)
Dear Kevin,
After my last letter to you, I got out my psychometric files and worked out the cutoff criteria for admittance to the Mega Society. I found two: a raw score of 22 or above on the non-verbal part of the Mega Test, or a score of 168 on the LAIT (or above) and a raw score of 19 or better on the verbal part of the Mega Test. I haven't enough data to make determinations about other tests.
. . .
Many people at the very limits of intellectual ability have personality disorders of one kind or another, though few if any are psychotic.
. . .
It's a big problem: the sane ones aren't bright enough to want to be with, and the bright ones aren't sane enough to be around either.
I believe that super-high-IQ societies attract aberrant personalities. I'm currently working--temporarily--for the National Science Foundation, and I'm surrounded by these three- and four-sigma minds who are extraordinarily sane, and so meek that I find it difficult to understand how they survive in the real world. They all have the demeanor of monks in a monastery. The other day I called one scientist a sorceror to his face and, with a big grin, he agreed that that was exactly what he was.
Does any member of the Mega Society ever smile?
4-28-98
Dear Kevin,
You may publish these numbers if you wish. I worked them out many years ago but was reluctant to publish them because of the small sample size (N=46).
There are two kinds of factor analyses extant in psychometrics: Principal Components Analysis and Common Factor Analysis. Common factor analysis is the preferred method.
What I did was to factor analyze the correlations between the LAIT and 24 Verbal items on the Mega Test, with 12 Spatial items, and 12 Numerical items. I found two important factors: the first column represents g loadings, and the second is a verbal/non-verbal bifactor.
| I | II | |
| LAIT | .76 | -.36 |
| Verbal | .44 | .47 |
| Spatial | .84 | -.09 |
| Number | .74 | .18 |
Rotating these factors to orthogonal simple structure, we get ``fluid intelligence'' and ``crystallized intelligence.''
| I | II | |
| LAIT | .83 | .11 |
| Verbal | .12 | .63 |
| Spatial | .75 | .38 |
| Number | .52 | .55 |
I hope these numbers are of some use to you.
7/27/98
Dear Kevin,
I have enormous respect for Arthur R. Jensen, but that doesn't mean that I endorse his opinion about the primacy of g. As I read his books and articles, it seems to me that even he fudges his views. He differentiates, for example, between fluid g and crystallized g. He also describes the method for making this differentiation as extracting common factors, making an oblique rotation, then doing a factor analysis on the correlations between axes, and if this results in two factors, then calling one fluid g and the other crystallized g. But I've noticed that what he does in practice is to extract common factors, then rotate them to orthogonal simple structure. If he gets two big factors, he sometimes calls them fluid g and crystallized g, but sometimes he calls them spatial/mechanical and verbal/educational.
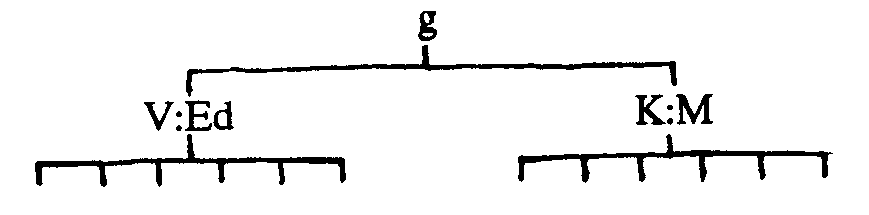
Take, for example, the correlations between the six Primary Mental Ability Tests reported on page 215 of Bias in Mental Testing. Take a common factor analysis of this data, then rotate the results to orthogonal simple structure. If you think that two factors cover the data, then this is what you will get.
| V:Ed | K:M | |
| Numerical | .61 | .24 |
| Word Fluency | .70 | .10 |
| Verbal Meaning | .69 | .12 |
| Memory | .50 | .12 |
| Reasoning | .67 | .43 |
| Spatial | .13 | .68 |
Note that reasoning is a pretty good measure of both V:Ed and K:M.
I've looked at the same data that Dr. Jensen has, but I see three rotated factors instead of the two Dr. Jensen did.
| V:Ed | K:M | Q:Ed | |
| Number | .16 | .20 | .73 |
| Word Fluency | .53 | .06 | .47 |
| Verbal Meaning | .58 | .09 | .40 |
| Memory | .64 | .11 | .07 |
| Reasoning | .47 | .40 | .52 |
| Spatial | .09 | .68 | .14 |
Again, reasoning is the most general test of all three group factors. But this time, there are three different kinds of ``intelligence'': verbal, spatial and quantitative.
The reason I'm writing this letter is to inform you how my research has placed the LAIT and the Mega Test in this pattern. Virtually no mental ability test measures the K:M (spatial/mechanical) ability factor, and that includes both the LAIT and the Mega Test. While there are three or four truly spatial items on the LAIT, they aren't very difficult and therefore don't show up as a special factor. The Mega Test, of course, has only one true spatial item on the whole test--item #36.
What my research shows, in fact, is that at gifted levels there are two different kinds of intelligence: verbal/educational and quantitative/educational. This is the same pattern found on the SAT-Verbal and SAT-Quantitative (or GRE-Verbal and GRE-Quantitative).
My factor-analytic studies of the LAIT and Mega Test show that the verbal subtest of the Mega Test is a good test of verbal/educational ability but isn't outstanding.
On the other hand, the quantitative subtest of the Mega Test may be the best measure of general quantitative reasoning of any test ever constructed. Hardly surprising, considering how many items Dr. Hoeflin ``borrowed'' from Martin Gardner's puzzle books and articles. The LAIT is only slightly behind the Mega Test non-verbal on quantitative/educational ability, and didn't borrow anything.
So, the LAIT is a near equal of the Mega Test nonverbal subtest, but is no measure of verbal ability at all. This leads to some unexpected results. My analysis of the Mega Test shows that it is mostly verbal in the lower range, about equally verbal and mathematical in the middle range, and mostly quantitative (mathematical) in its higher range. The LAIT is pure mathematical throughout.
Mensa and ISPE selected members using verbal/educational IQ tests. TNS and Four Sigma initially took Mensa and ISPE members and selected out the most mathematical. Later, they selected people who were quantitatively gifted from the general population. People who were preselected from Mensa have different kinds of minds than those selected from the general population, though both may have ended up in Triple Nine and Four Sigma.
Don't dismiss this out of hand. Remember that mathematical thinking is not about numbers: it's about patterns.
8/24/98
Dear Kevin,
I know you never listen to me, but for once try to keep an open mind. I have something to teach you about factor analysis that took me a very long time to reason out, and which neither Dr. Jensen nor any other psychometrics researcher is likely to tell you. Perhaps they don't actually know, though somehow I doubt it. Let me tell you why researchers can't agree among one another about whether intelligence is one thing or many.
Let's take a hypothetical test and give it to a hypothetical norming sample. This hypothetical test includes every kind of mental ability item ever found useful, each kind grouped into subtests with very low floors and very high ceilings. Each subtest has a very high internal consistency reliability (KR-20).
Now give this hypothetical test to 100,000 hypothetical subjects, take the correlations between the subtests, and factor analyze the results (principal factors--also called common factors). What would we find, hypothetically?
What we would find is one large general factor about twice as large in terms of variance as the sum of all the other sources of variance combined. We would find half a dozen to a dozen smaller factors (or bifactors), and an error factor accounting for about five percent of total variance.
Now take the same test, but instead of factor analyzing the full range of scores, factor analyze only the top 25 percent (roughly an IQ of 108 and above). Now you get different loadings. The large general factor goes down, but is still pretty large, while the special factors grow in size, and so does the error variance. But two or three of the special factors grow much more than the others.
Finally, do the same procedure on the top one percent. Now the general fac-tor and the two or three biggest special factors are the same size. There is no longer a general factor.
People who believe in a large general factor--such as Dr. Jensen--base their findings on a broad spectrum of ability drawn from the general population.
People who believe in Vernon's hierarchical model of intelligence. Namely:

draw on range restricted data.
This model of intelligence was elicited from data supplied mostly by college students (roughly the top 25 percent of the IQ spectrum).
At still higher levels, g becomes small enough that we now have three coeval intelligences: fluid intelligence, crystallized intelligence, and spatial/mechanical ability. These are the same three major factors discovered by Horn and Cattell when they first named fluid and crystallized intelligence. They are also the three most important factors that turn up when I factor analyze Thurstone's Primary Mental Abilities. (The description of factors given at the bottom of page 215 in Bias in Mental Testing is wrong.)
This has implications for the super-high IQ societies. Should the super-high IQ societies concentrate on only one of these as the true intelligence? Should there be a weighted or non-weighted average of two of them, or perhaps all three?
What we've done in the past is stress crystallized intelligence--Mensa to some extent, and ISPE very heavily. Triple Nine and Four Sigma tried to rectify that imbalance. The Mega Test was an attempt to weld two entirely different kinds of mental ability into a non-coherent whole.
Nobody has ever truly attempted to measure spatial/mechanical ability at super-high levels. Experiments have shown that some people can actually be taught how to visualize in four dimensions. I get glimmers of it myself when doing factor analytic studies. No super-high IQ society selects for this ability.
Frankly, I can't see why this needs explanation. It should be perfectly obvious to anyone that Shakespeare could never have done what Newton did, nor could Newton have replaced Shakespeare. Nor could either of them have replaced Edison or van Gogh. The verbal form of intelligence took preeminence from the first days of intelligence testing because it predicts literacy and the literate run the world. Literate people are the organizers and manipulators--politicians, preachers, lawyers, CEOs, etc. Only in the last quarter of this century--because of computers--has the balance of power shifted in favor of pure puzzle solvers--the high level ability tapped by the LAIT or Mega non-verbal scales.
The only high-IQ society I ever truly enjoyed belonging to was Triple Nine. Most of them were or had been members of Mensa, so they were pretty high in verbal intelligence. Then the LAIT sifted out the very best puzzle solvers from this pre-selected verbally gifted group. They were fairly well read, but not overly burdened with educational credentials. They were broadly educated, but not deeply trained in some all-consuming specialty. They had no genius, but common sense was as ubiquitous as dirt. I liked them a lot, and miss them still. It's too bad that the invasion from ISPE was allowed to destroy the best of the best.