Hilbert Matrix Analyses
Ronald Yannone
In my work I use MATLAB (stands for matrix laboratory) for systems engineering design and modeling. MATLAB is a high-performance language for technical computing, developed by MathWorks, Inc. MATLAB integrates computation, visualization, and programniing in an easy-to-use environment where problems and solutions are expressed in familiar mathematical notation. My software “library” includes MATLAB version 5.1, the Signal Processing toolbox, Statistics toolbox and Symbolic Math toolbox.
I took some time to perform some preliminary analyses of Hilbert
matrices using the Symbolic Math toolbox. The first four Hilbert matrices are:
| Hl = [1] | H2 = [1, 1/2] | H3 = [1, 1/2, 1/3] | H4 = [1, 1/2,1/3,1/4] |
| [1/2, 1/3] | [1/2, 1/3, 1/4] | [1/2,1/3,1/4,1/5] | |
| [1/3, 1/4, 1/5] | [1/3,1/4,1/5,1/6] | ||
| [1/4,1/5,1/6, 1/7] |
If we add all the reciprocals of each element in a Hilbert matrix, a nice pattern results.
Applying this to the first 10 Hilbert matrices, we get the first ten terms of the
sequence:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000
These are the cubes of the natural numbers. If the cumulative sums of the numbers in this sequence are computed, we get a new sequence, whose first ten terms are:
1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025
These are the squares of the triangular numbers [numbers of the form (n2+n)/2]. If we add all the squares of the reciprocals of each element in a Hilbert matrix, we get the first ten terms of the sequence:
1, 18, 93, 296, 725, 1506, 2793, 4768, 7641, 11650
Taking successive differences of this sequence four times results in
constant differences of 28. The resulting 4h-order polynomial expression is:
1 |
|
_ |
[7N4 - N2] |
6 |
If we take the reciprocals of the elements of the Hilbert matrix, square the resulting
matrix, and compute the sum of all the resulting elements in the product, we get the first
ten terms of the sequence:
1, 34, 261, 1104, 3375, 8406, 18179, 35456, 63909, 108250
Taking successive differences of this sequence five times results in
constant differences of 130. The resulting 5h-order polynomial expression is:
1 |
|
_ |
[13N5 - N3] |
12 |
If we take the combined sum of the main and anti-main diagonals of the reciprocal Hilbert
matrix elements, we get the following first ten terms of the sequence:
2, 8, 18, 32, 50, 72, 98, 128, 162, 200
Taking successive differences twice results in constant differences of 4. The resulting 2nd-order polynomial expression is:
2N2
Returning to the first four Hilbert matrices, we can see an interesting feature in the structure of the rows (or columns) of the Nth order Hilbert matrix. Namely, we see that the first row (or column) are the Nth harmonic numbers. The first four harmonic numbers are:
H1 = 1, H2 = 1 + 1/2, H3 =1 + 1/2 + 1/3, H4 = 1 + 1/2 + 1/3 +1/4
In general, the nth harmonic number is
Hn = 1 + 1/2 + 1/3 + . . . + 1/n
No harmonic number is a whole number after the first one: look at the term with the highest power of 2 in it. It has nothing with which to pair. So, H2, H3, H4, . . . have odd numerator and even denominator. A closed form approximation for the nth harmonic number is given by
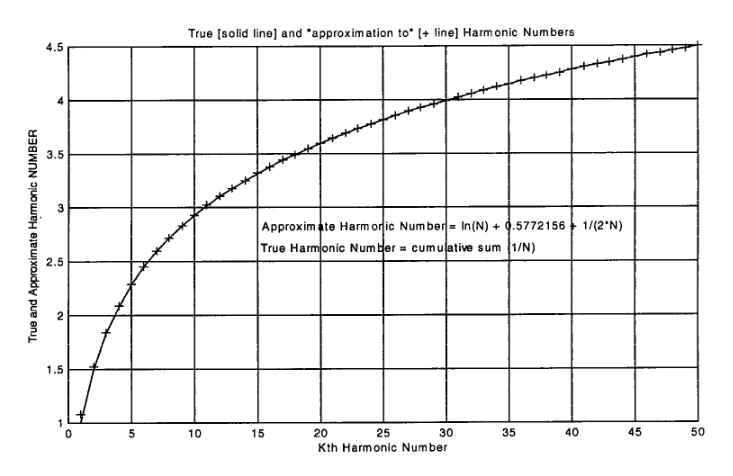
Hn = ln(n) + gamma + 1/2n,
where gamma = 0.577215664901532860606512, the Euler-Mascheroni numher.
The first 50 true and approximate harmonic numbers are plotted in Figure
1 and the error (difference) between them is shown in Figure 2.

Figure 1. The First 50 True and Approximate Harmonic Numbers
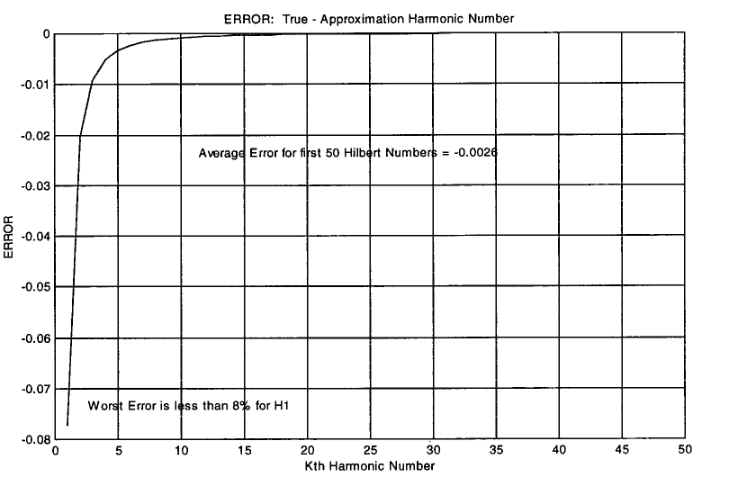
Figure 2. Average Difference (Error) for the First 50 True and Approximate Harmonic
Numbers
The successive rows (or columns) in the Hilbert matrices are larger harmonic numbers—the summation of the first “so many” harmonic numbers. E.g., in the second Hilbert matrix, the first row “houses” the second harmonic number: 1 + 1/2 = 3/2. The second row “houses” the third harmonic number minus the first (i.e., no 1 term), or 1.8333 (3rd harmonic number) - 1 = 0.8333—which is 1/2 + 1/3.
The sum of all elements in the first 20 Hilbert matrices are:
| 1.0000 | 2.3333 | 3.7000 | 5.0762 | 6.4563 | 7.8385 | 9.2219 | 10.6059 | 11.9905 |
| 13.3754 | 14.7606 | 16.1459 | 17.5314 | 18.9170 | 20.3027 | 21.6885 | 23.0744 | 24.4602 |
| 25.8462 | 27.2321 |
There are probably many more interesting properties of Hilbert matrices. If you know of any, please share them with us. Thanks, Ron Yannone
See the MATLAB code for the analysis reported in this article, item 15 in this issue.