Reply to Chris Cole on Norming High-Range Tests
Dean Inada
In order to implement Chris's suggestion [Cole "How to Protect High-Range
Tests," Noesis 155 (2001): 8-9] of tests consisting of a small subset of a
larger set of questions, we'll want a better method of norming the tests than simply
ranking people by the number of questions they get correctly, since one person may be
asked harder questions than another. I suggest a method that tries to estimate for each
question the probability of getting it right or wrong as a function of a person's
percentile rank in the population, this rank is estimated by multiplying the generally
increasing and decreasing functions for the problems gotten right and wrong. Bootstrapping
the estimates, by starting with a slope 1 straight line as an initial estimate for the
probability of getting a problem right and a slope -1 line as the probability of getting
it wrong, is equivalent to just ranking each person based on the proportion of correct
answers.
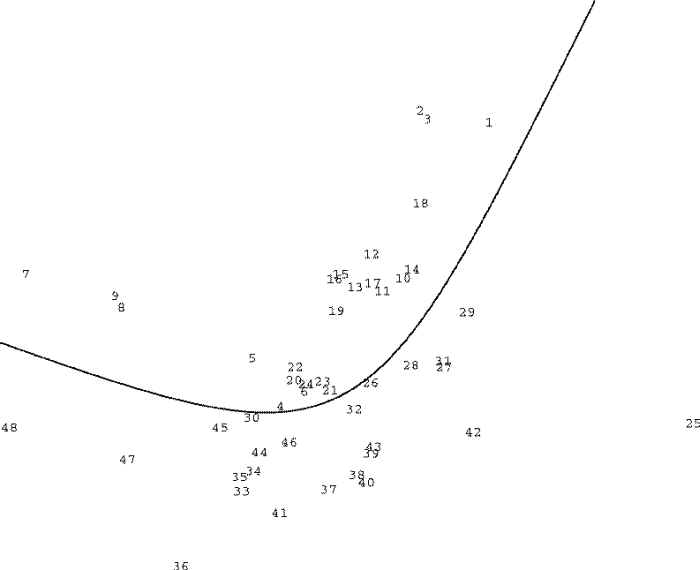
To test out this method, I tried taking the existing Mega Test scores vs. problems missed data from
http://www.eskimo.com/~miyaguch/megadata/item_ana.html
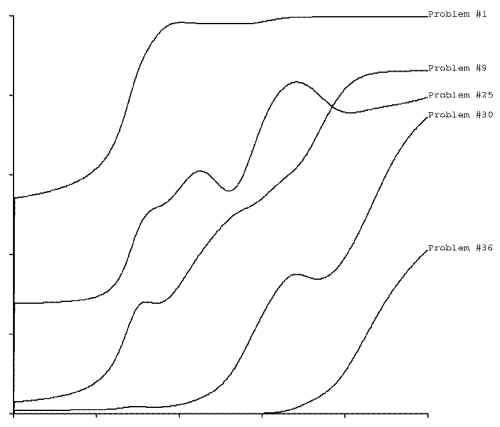
And when the iterations stopped changing, I had functions like:

Multiplying the appropriate functions for a given person's answers gives a distribution of
that person's expected percentile rank within the population. Multiplying a bunch of
increasing and decreasing functions tends to look like a Gaussian, as you might expect.
The more questions we ask, the more functions we have to multiply, and the width of the
distribution gets narrower.
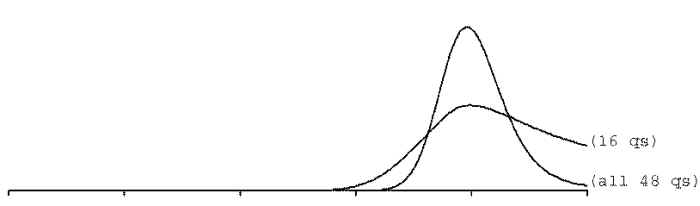
(But even using all 48 questions the distribution still seems wide if you want to
distinguish test takers at the 99.9999%ile.)
Problems with a function flat at the high end, such as #1, are not very useful for
discriminating the high ranks and problems with a function flat at the low end, such as
#36, are not very useful for discriminating in the low ranks. By choosing problems to ask
whose greatest slope is in the range of our current estimated rank distribution we can
more efficiently narrow down the rank estimate.
Multiplying the probabilities incorrectly assumes that each question is independent, but
that may not be too bad since much of the correlation between questions is due to both
being correlated to percentile rank within the sample populaton.
Clustering the questions by relative correlation (x tries to be closer to y than to z if x
is more closely correlated with y than to z) we find one axis roughly proportional to
problem difficulty, and the verbal analogies tending to cluster in one quadrant.