Reply to Ron Hoeflin on Intelligence
Scales
and High-IQ-Society Admission Cutoffs
Kevin Langdon
I have no idea why Ron Hoeflin thought it would be a good idea to rearrange the cutoffs for the higher-IQ or "beyond-Mensa" societies, as proposed in "Comparing 'Normal-Curve' (Galton) vs. 'Original Stanford-Binet' (Terman) Scales of Intelligence" in Noesis #163. I respect Galton's pioneering work leading to the foundation of the science of psychometrics, but there's no particular virtue to slicing up the normal curve in just his way and no other.
The societies' cutoffs are spaced appropriately, in my opinion, with the major societies in a very simple 2, 3, 4 sigma progression, breaking down at the high end with the Mega Society, at 4.75 sigma (but the selectivity ratios do not reflect this irregularity; they are roughly 1000/50 = 20, 30,0000/1000 = 30, and 1,000,000/30,000 = 33).
The One-in-a-Thousand Society (or the Triple Nine Society) would become more than 2.5 times less selective under Dr. Hoeflin's proposed revision of cutoff levels. The Prometheus Society would become about 7.5 times less selective. And the Mega Society would become 15 times less selective--but people join these societies precisely because of their selectivity!
Why would members of the societes be inclined to vote for Ron's proposed cutoff changes? This reminds me of the time Ron tried to raise Mega's admission standards and demote 3/4 of the membership to "honorary member" status, which, not surprisingly, did not receive majority support from the Mega membership.Dr. Hoeflin wrote:
To establish the minimum cut-off for groups like the Prometheus Society and the Mega Society, the nominal requirements are 164 IQ (4.0 standard deviations above the mean) and 176 IQ (4.75 standard deviations above the mean), respectively. But we have to choose between the Stanford-Binet interpretation of these scores and the normal-curve interpretation.
We chose long ago, as clearly indicated by the IQ/normal-curve correspondences provided by Dr. Hoeflin above. Our qualifying scores--and those of other high-IQ societies--are defined in terms of percentiles, and when IQ is spoken of in this context what is usually meant is deviation IQ.
Eysenck's calculations appear to be somewhat inaccurate here. The one-in-a-thousand-million level is about 6 standard deviations above the mean on the normal curve, which would correspond to 200 IQ only if Eysenck were assuming 16.67 IQ points per standard deviation. But the 32 in a million level is 4 standard deviations above the mean on a normal curve, which would be 160 IQ only if Eysenck were assuming 15 IQ points per standard deviation, not 16.67.
Hoeflin's calculations are somewhat inaccurate too. The one-per-billion level is reached at about 5.85 SD's above the mean. This would only make it worse for Eysenck, as it would imply an SD of about 17.
Mega members Keith Raniere and Dean Inada have developed a means of pinpointing the mega (=one-in-a-million) level or other specific percentile levels on an intelligence test by utilizing the percentage of people who can solve progressively more difficult problems in the test.
Presumably, they're not doing this by administering the test to a large random sample of the human population. What sampling procedure is used, what statistical model is employed, and what are the details of the algorithm? Keith and Dean, I'm interested in seeing your material. I invite you to submit something for the Journal of Right Tail Psychometrics, to begin publication on the Web within the next few weeks, under my editorship.
But this approach seemed to me to put the mega level on my Mega Test too low, e.g., as low as 39 or 41 right out of 48. My own estimate put the one-in-a-million level at 43 right. Kevin Langdon, by using a crude straight-line norming from the bottom of the test to the top, thought the one-in-a-million level should be even higher, namely 46 right out of 48.
I'm willing to allow one point for ceiling-bumping for scores within a point or two of a test's ceiling. See:
http://www.polymath-systems.com/intel/hiqsocs/megasoc/noes140/langdon.html
However, I consider any further departure from straight-line equating to be highly questionable and it is unlikely to be accepted by most psychometricians.
If we average 39 and 41 we get 40, and my own estimate of 43 is exactly midway between this average Raniere-Inada figure of 40 and Langdon's figure of 46. If we retain our current claimed admission standard of one-in-a-million rather than adopting the proposed new 15-in-a-million standard, then I suggest we continue to use my own moderate figure in preference to the other ones.
If we set our qualifying level by means of numerology that would make a lot of sense, but I suggest that we examine the statistical evidence instead.
At any rate, we need to vote on whether to adopt the proposed new standard of 15 in a million or retain our current standard of 1 in a million. Any comments should be sent to me promptly for inclusion in the next issue or two. In the absence of comments, I will call for a vote in the next issue. I reserve the right to voice my opinion on any comments in the issue in which they appear. Members are intelligent [enough] to sort out which viewpoints seem the most plausible given the current state of our knowledge. But I don't rule out extended discussion of the cut-off issue if there is sufficient interest in debating it.
The Editor is attempting to reserve a right he doesn't have. He's saying that he reserves the right to put his thumb on the scale used by Mega to weigh its options, by allowing himself the opportunity to have the last word on whatever comes up for a vote. It's all right for the Editor to put in his two cents' worth in ordinary debates, but it isn't right for him to have such a disproportionate influence on Mega Society decision-making.
In his "Editor's Notes" in Noesis #165, Dr. Hoeflin wrote:
In this issue I am publishing 15 pages of SAT data that a former Mega member, Keith Raniere, obtained from the chief Educational Testing Service statistician covering the precise distribution of SAT scores (verbal plus quantitative combined) for the years 1984, 1985, 1986, 1987, and 1988. Graphing these distributions for any given year or for all five years combined yields a distribution that differs markedly from the distribution curve given by Chris Cole on page 4 of the previous Noesis. Specifically, his graph shows no elongated tails at each end of the graph but seems to assume that tens of thousands of people are hovering within a stone's throw of a perfect 1600 and could have attained or missed the 1600 mark by a few slips of the #2 pencil. Even Chris' own data for post-1995 SAT scores on page 6 of the previous issue when graphed yields elongated tails that are at sharp variance with his graph on page 4. And this is despite the fact that the Educational Testing Service "dumbed down" the SAT after 1995, lopping off about 70 points of ceiling so that 1600 on the pre-1995 SAT equals about 1600 on the post-1995 SAT.
This is obviously an error. The sentence should read: ". . . so that 1600 on the post-1995 SAT equals about 1530 on the pre-1995 SAT."
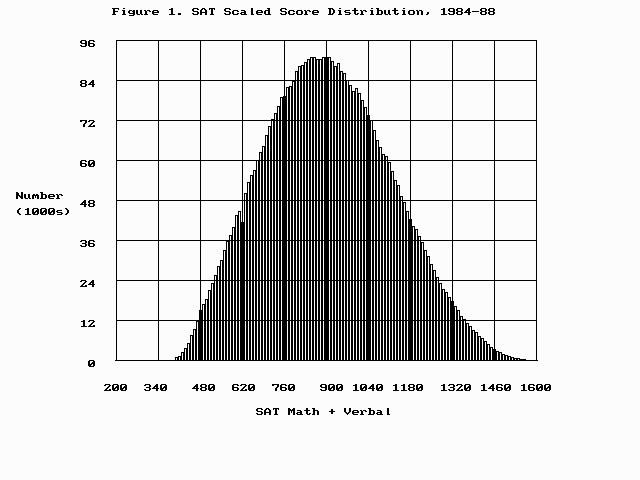
Graphing the data provided by Ron Hoeflin in this issue yields a curve with a truncated left tail (Figure 1). The dropoff at the bottom end is an artifact of the multiple-choice testing procedure with its penalty for guessing, as is the larger number of 1600's than 1590's. Raw scores are computed using plus 4 units, on a certain scale, for each item correct, and minus1 unit for each item wrong. As there are five answer choices, someone who knows absolutely nothing about the material being tested for will earn a score of 0, on the average.
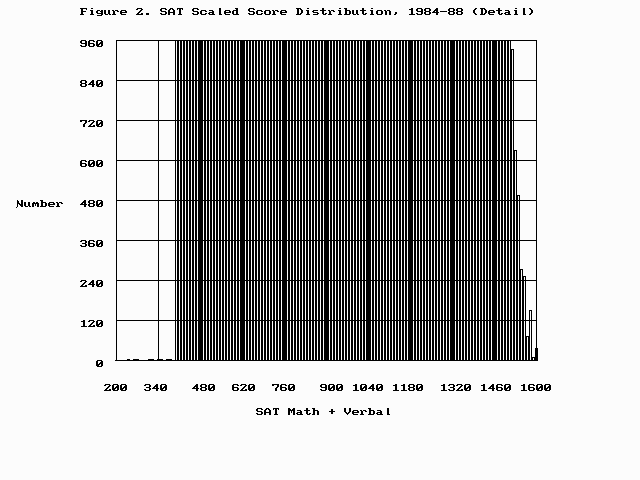
Scores are reported to testees, on a scale from 200 to 800, for the Mathematics and Verbal sections. The minimum individual total is 400, but a few testees have actual totals below this (one must be both unastute and unlucky to score that low). Scores below 200 are reported as 200, but including these "below zero" scores is useful for statistical purposes. This distorts the left tail of the distribution, but it's the right tail that's of the most interest to us. The right tail is only foreshortened above about the four-sigma level--as is apparent in the view of Figure 2, in which the vertical scale is magnified by 100--but that's important for Mega admission purposes..
Dr. Hoeflin continued:
A friend of mine who scored 1540 on the SAT as a high-school junior seems to have shared Chris's misapprehension about the shape of the SAT distribution curve, for when I asked her to guess how many people out of a bit over 5,000,000 high-school seniors who took the SAT from 1984 through 1988 had scores 1540 or above, her guess was 250,000. The actual number was 1,282 So much for the tens-of thousands-teetering-on-a-perfect-score myth.
Figure 2 shows that the number of high scores does drop off suddenly at the high end.
So much for anecdotal evidence.
The way we interpret test scores is important not just for admitting members but also to the way we're perceived by the outside world. These societies will be "discovered" soon, on a scale far beyond the press attention they've received to date; it wouldn't be prudent for us to make wild claims that could be used to dismiss us as a serious organization.
Admittedly, attempting to select members at the one-per-million level is pushing the envelope at the current state of the art of psychometrics, but despite the uncertainties it's up to us to make the most reasonable determination we can of where our cutoff should be.
If the Mega Society were to lower its percentile standard for admission, that would leave the Pi Society, which uses very questionable tests for admission purposes, alone in the niche that we'd foolishly abandoned.
Although the Mega Society is less active than some other high-IQ societies, this is only to be expected, in view of our relatively small numbers. It ain't broke. Please vote "no" on Dr. Hoeflin's proposal to lower our admission standards.