Member Ray Wise has apparently moved. His copy of the last issue of Noesis was returned with notice of expiration of forwarding instructions. If any other member has his new address, he (or she) should send it to me or to James Hajicek, who has considerately been providing address labels.
I recently got a letter from Ron Hoeflin. This letter, which was apparently written before he had finished reading issue #44, is partially concerned with matters of policy. My response will follow the section on metagames.
I must tentatively qualify a statement made in Noesis no. 44 concerning a policy attributed to Martin Gardner. On the chance that my source might have been inaccurate, I mailed a copy of that issue to him with a covering letter. His response suggests that the policy either never existed or has been revised; as to which, his letter leaves some doubt. Regarding the paper on Newcomb's paradox, he prefers to withhold his comments pending more thorough evaluation. In the mean time, he thoughtfully provided copies of his most recent remarks on the subject, as well as an extensive bibliography. This bibliography is twenty-seven entries long, and covers the period from 1969 to 1985. It indicates that this paradox, of which I understand some members had never heard prior to its mention in Noesis, has been a hot topic in philosophy for over twenty years. To let those members unfamiliar with the history of Newcomb's paradox get some idea of its notoriety, I have taken the liberty of including the bibliography in this issue (pp. 11-12).
Because I usually work from basic principles, very few of the entries in this list played any part in my thinking. However, one cannot help but notice that the theory of "metagames" figures in several of them. This theory, with which I am familiar enough, involves joint functions of subjective utility. There are certain situations, including the famous prisoner's dilemma, in which the maximization of collective utility is inconsistent with reasoning based on individual self-interest. Some n-player games can have more than one winner; ND's 2-player game can obviously have two, and in fact must have two if the outcome is not to be severely unfavorable to either player. Consider the Newcomb payoff matrix
| ND: predicts black box | predicts both boxes|
Subject: |------------------------|--------------------|
takes black box | $l,000,000 | correct | $0 | incorrect |
----------------------------------------------------------------|
takes both boxes | $l,001,000 | incorrect | $l,000 | correct |
|------------------------|--------------------|
and note that the upper left entry is the only joint optimum, given that ND places a high premium on his unbroken veracity.
Observe also that the expected utility argument, as presented in Noesis no. 44, favors different moves according to whether mm does or does not have significant confidence In Nil's predictive powers. If he does not - even in the face of all the evidence - then he might regard ND's move as virtually random with respect to his own choice, thus in effect denying any mechanism of dependency between what ND does and what he does. This may cause him to assign equal probabilistic coefficients to both of ND's possible moves, which causes the sum of the expectations in row two of the matrix to exceed that of row one (of course, this casts considerable doubt on ND's own rationality, given the arguments presented in The Resolution of Newcomb's Paradox).
If MN is thinking rationally even in his own light, he will at least see ND's perfect record as evidence that ND is a master of both human nature and decision theory. Specifically, MN will suppose that ND is somehow gauging his own level of intelligence and rationality, and - finding it high - will use it to "simulate" MN's calculation of strategy using abstract game theory. Thus, MN will reason to the conclusion that both he and ND will be applying game theory to the formation of strategy. While this is not the same mechanism of dependency contained in G, it is a median ism nonetheless.
Now, constructing the above matrix, MN will naturally observe that his no-confidence application of expected utility leads him initially to a move which is not a joint optimum (i.e., that in the lower left corner of the matrix). He also knows that ND, who may well suspect his lack of confidence, can apply the minimax principle to "cut his losses" given the likelihood of this move. Observe that minimax is a "metarule" relative to expected utility; it uses the viewpoints of both players to the advantage of one. Here, it causes ND to choose column two. Unfortunately for MN, the intersection of row two with column two occurs at an outcome decidedly unfavorable to him. Moreover, MN cannot at this point improve his lot by switching moves; the intersection of row one and column two is even worse than the entry below it. The game has reached a strategic equilibrium, which in its present guise seems more to him like a game-theoretic dead end.
What should MN do now? He is dead set against any revision of his disbelief in ND's prescience; furthermore, he considers it hypocritical and infra dignitatem to "pretend" that he believes when in fact he does not. What if he should pretend, but ND should fail to take account of it? Then ND stays with column two while he switches to row one, and both lose everything. Even if ND takes account of his is pretense and switches to column one, MN has effectively confirmed his "prescience". This bothers MN, even though this kind of prescience is not quite as repugnant to him as a spin through G program-space. He has still been manipulated on the basis of his own perfectly predictable reasoning, and is quite within bounds to regard this as an unsatisfactory glorification of his supposed "free will". Therefore, he resolves to "pretend to pretend", switching back to row two after ND obligingly switches to column one. This seems rational in any case, since the switch is worth an extra $1000 to MN.
Notice that we have been led into another computative regression, this one even less tractable than the one we have previously defined as "G". On the basis of what MN considers to be perfectly rational assumptions about the nature of this game, game theory has led him in a circle that may repeat endlessly in a spider-and-fly parody of the Turing halting problem. In this twist on the old paradigm, each of two automata tries to determine the programming of the other from output simulated according to circular premises to which it is assumed to conform. Returning to the symbolism of the Resolution the state-transition functions dM, dMD, have become determinate but circular, whereas mM, mMD remain mutually uncertain, and in fact nondeterministic relative to this low-level version of standard game theory.
Enter the theory of metagames, which involves the construction of extended matrices by adjunction of "conditional strategies". The moves in such a matrix are "metamoves" which cover every possible contingency; each possible move by one's opponent is regarded as one cell of a linear array whose contents vary over all repetitive permutations of countermoves. E.g., take an arbitrary one-move, two-player game in which each player has possible moves x or y. The conditional strategy for player 1, "xx", means: "if 1 were to expect 2 to make move x, then 1 would make move x; if 1 were to expect 2 to make move y, then 1 would make move x." In this case, 1 has four conditional strategies xx, xy, yx, and yy. The next extension is formed analogously: given l's metamoves, 2's counter-strategy "xxxx" means: "if 2 were to expect 1 to choose xx, then 2 would choose x; if 2 were to expect 1 to choose xy, then 2 would choose x; similarly, yx1 —> x2; yy1 —> x2." Where the original matrix is regarded as step one in this progression of extensions, the metamatrix for step n ≥ 2 consists of 22n-1 x 22n-2 entries. This exponential blow-up will finally reveal all possible equilibria, including the mutually favorable ones. Further extension becomes unnecessary when new equilibria cease to appear in the matrix, or when the set of equilibria reaches "closure".
The first metamatrix for Newcomb's game is as follows (where move A means "take (predict) the black box only", move B means "take (predict) both boxes", the rows are MN's possible strategies, the columns are ND's conditional strategies, and the starred cell represents a mutually favorable equilibrium):
ND: AA AB BA BB --------------------------------------------------- | correct |* correct *| incorrect | incorrect | A| $1,000,000 |* $1,000,000 *| $0 | $0 | |--------------|--------------|------------|------------| B| incorrect | correct | incorrect | correct | | $1,001,000 | $1,000 | $1,001,000 | $1,000 | ---------------------------------------------------------
On the (by no means solid) premise that an arbitrary subject has the wit, time and inclination to reason this far, the lopsided equilibrium described for the base matrix becomes inconsistent with reasoning motivated strictly by individual self-interest in light of mutual uncertainty. It is now apparent to MN that ND will choose conditional strategy AB in any case, since he thereby wins no matter what MN does. So MN must choose A. The intersection of A and AB is not only a joint optimum, but an equilibrium from which neither can make an advantageous switch. Individual self-interest is now logically consistent with joint utility.
If Newcomb's paradox were reducible to the superficial conflict between individual and joint calculations 0f utility, the theory of metagames would be the key to resolution. The theory has justly been praised as the logical equivalent of the golden rule, and even as a cure for the sneaky, self-interested game theory so long practiced by the cold warriors in top-secret military think-tanks. Unfortunately, there are at least three aspects of the problem which cast doubt on the solutative adequacy of metagames.
First, certain ingredients of the Newcomb formulation make it impossible to apply the theory retroactively to all of ND's former victories. The "plausible distribution" of players with respect to their moves indicates that their choices were reached by various rationales. These must necessarily have included rationales which did not take account of the theory, or which included it merely as one phase of a more complex train of thought. This latter possibility leads to the second inadequacy of metagames.
That is, the metagame scenario continues to involve the players in a computative regression dangerously like that of the classic Entscheidungsproblem, wherein each player is trying to compute the computative power and programming of the other. After all, there is nothing to prevent one player from capitalizing on what he presumes will he the other's good-faith adherence to the metagame collectivization of utility. If ND doubts MN’s reliability on this score, he will probably fixate on base column two (not much of a "solution" from MN's viewpoint). In many other such games, if each player suspects a "rat" in the other's programming, the regression can continue forever...provided, of course, that no effort is made to elevate one or the other from G0, the physical level, to G1, the level of programmatic constraint on G0, (note that if strategic collectivization were enforced by projection from the programmatic level, defection would be impossible, and this would indeed ensure a joint optimum).
This brings out the third weakness of metagames: they cannot account for the G0, evidence confirming ND’s G1-status. The Newcomb paradox is ultimately one of prediction, and prediction paradoxes differ radically from those confined to the same G-timetype. This is in fact the distinctive feature of Newcomb's paradox, and it is impossible to claim resolution without addressing it. But that is apparently the position in which some claimants find themselves. With due respect to their insights, the resolution in #44 stands well above any based on game theory alone.
I recently received a handwritten letter from Ron Hoeflin, which contains permission to quote. I'll address its points in the order they were made, with the exception of some remarks on the paradox; these require a more detailed response. I must own to being a little confused by some parts of this correspondence. If any of what follows seems low on enthusiasm, please chalk it up to my confusion .
First, he prefers to keep the journal on a monthly schedule. So, I assume, does everyone else. Noesis #44 was dated "December-January" for a number of reasons. The most important of these was that it was not ready until late January; it had to lie completely rewritten after I decided to serialize the content of the original draft. Just as important, it contains the solution of a famous and complex problem - a "first" for Noesis - and may require more time for absorption by those members unfamiliar with its key concepts. It thus seems inadvisable to follow it up too quickly. As some readers may recall, this is not the first time a month has been lost; the August-September 1989 issue also covered such a gap, and several other issues have been delivered well behind schedule. Nevertheless, #45 will - at Mr. Hoeflin's request - be redundantly dated. The February issue will be completed as time permits.
Second, Mr. Hoeflin remarks that "the lack of a strong central editor tends to turn each issue Into a monologue on the part of the person responsible for that issue, which I do not consider entirely satisfactory". This is true, as far as it goes. But there are several other important considerations that it ignores. The most salient of these is probably the distinction between "strong" and "qualified". It is sometimes not easy for those who lack the right background to grasp the complex issues that might be expected to occupy the thoughts of extremely intelligent people. As a case in point, the debate over Newcomb's paradox - a matter that I could have settled definitively at the outset - went on for two years before being laid to rest. And this is by no means the only such example.
"Monologues", regardless of what anyone thinks of them per se, are not always avoidable or even undesirable. The history of science, mathematics, and philosophy is one monologue after another, more or less...the point being that an informed monologue outweighs any cacophony of inflexible opinions. Nor are monologues entirely the fault of the editors In whose issues they may have occurred. I have not heard of any past editor of Noesis failing to relay the opinion of any member who saw fit to offer one. The fact is, many of the members of this group have been quite unyielding in their reticence. More active members will no doubt forbear to criticize them. If they may in turn be forgiven an occasional monologue to fill the silence.
Mr. Hoeflin - who acceded, along with Mr. Erlandson, to my provisional tenure as editor - states that if said editor cannot closely adhere to a schedule of monthly publication, he "would prefer to find somebody who can".
Regarding the case with which a willing and qualified editor might be found, it has already become obvious to many members that the job is not without its onerous aspects. At the risk of seeming gauche, I will give one example: the total monetary cost to me of printing and mailing issue #44 was approximately $40. This says nothing of the cost to me in time for research and compilation. At least two central editors - Messrs. Hoeflin and Erlandson - have previously intimated the difficulty of producing a steady flow of interesting material in the absence of input from other members. As a favor to the Society, I am willing to assume responsibility as long as it intersects with certain other priorities, and only as long as I feel appreciated for my effort and expense. If there is any disagreement about this, I will be only too happy to defer to whatever counterarguments are presented, regardless of their soundness or motivation. Any blame may settle where invited.
Mr. Hoeflin states that "if I resume the editorship myself, your essays will be published as rapidly as space (and your own submissions of material) permit". This would not be unreasonable under ordinary circumstances. But as my own situation is unique, I should probably point out once again that my past submission of material was severely constrained by uncertainty as to space. I can see no reason to relax that constraint, given that the above statement seems to reflect no change in past editorial policy. The possible effects that this would have on the long-term quality of the journal can at best be hazarded from past data. I see no point in pretending that what I recently contributed is not in certain respects preferable to much of the material which preceded it. If the other members are also indifferent to the distinction, then perhaps this exercise is futile, and another editor should be found before I waste more of my time and theirs. Noesis is a forum of convenience, not of last resort.
Next, it is suggested that Noesis will probably never become a "prestigious scholarly journal" without benefit of non-member subscribers, and that the question of whether to allow them should perhaps be put to a vote, contingent on returning to one central editor. This is probably a good idea, on the condition that such subscribers understand and agree to certain considerations along the lines of those reprised in the next several paragraphs.
Mr. Hoeflin goes on to express the opinion that the editor is "vastly overconcerned about plagiarism of original ideas by other members". I find this hard to follow, having in fact expressed trust in the members in my opening comments. This is probably a reference to the four-page letter I wrote last year, when the name of the society had just been changed to "The Hoeflin Research Group". This letter described a kind of occupational hazard faced by professional scientists and academicians, and contained no aspersions on the members of this group. This may be readily confirmed by anyone willing to review pages 13-16 of the last issue. How this letter relates to the Society is clear enough. Papers can get lost or mislaid; copies of the journal can get misplaced or passed around, conceivably ending up in the hands of people who may not share the sensibilities or qualifications of the authors or those for whom they were intended. And "plagiarism" is only one aspect of a more complex problem. My apologies to anyone else who got the wrong impression.
In the same vein, it is subsequently remarked that "if others carry your ideas forward, that is legitimate…" To this, however, it is necessary to add "...so long as they do not in the process avail themselves of facilities to which you are denied access." I have already carried these ideas forward rather thoroughly in many ways, and see no reason why others should try to duplicate my own results unless they are doing so because they suspect that I am in no position to claim them publicly, and wish to take unfair advantage of their own connections or credentials. But again, I am more concerned about publish-or-perish types than I am about the members of this group. If this group were the problem, it would not have been privy to my results. And the intrinsic importance of these ideas, as well as the matter of how to further develop them, will probably not be entirely obvious to anyone who has not applied prolonged effort towards understanding them.
One more word on the matter of access. The system of sponsorship and review means essentially that if a previously unpublished author of scholarly articles wishes to have his work published in any of the majority of "important" journals, he will be required nut only to provide personal credentials - which I never sought and which I consider utterly irrelevant to any meaningful evaluation of ideas - but in many cases to subjoin his own name to that of a better-known and more "reliable" collaborator, irrespective of the actual contribution thereof. This is a kind of hypocrisy to which I owe nothing and feel no inward obligation.
Those with academic credentials long ago arrogated the right to certify "truth" partly on the basis of its sources. This practice, some aspects of which may be traced back to prehistoric rites of domination, reached its present enlightened form with the rise of the medieval guilds. Historically, its effects have ranged from mildly beneficial to ludicrous and reprehensible. With respect to me, this policy happens to be weighted towards the bad end of the scale. Credentials can never "take the high ground" relative to truth, for truth is the only ground on which they can stand. As the highest use of intelligence is in the quest for truth, this applies uniformly to any political credentials derived from the history of this or any other society. I sincerely hope that this explanation will be deemed satisfactory by others who might think my comments eccentric, of whom I request only the allowance that I might know my own situation better than they.
Openminded members wanting to understand my position might like to take a look at the bibliography provided by Mr. Gardner. It depicts the projection of Newcomb's paradox upon a background of credentials. The image does ample justice to the source in point of irreconcilability and chaos; the one thing that most of these entries have in common - besides inadequacy - is rigidity. Students of human nature know that people are never so adamant as when they attempt to defend weak opinions. One might thus suppose that many of these authors would not welcome an "outsider" whose own views make theirs look even weaker than they already do. Now, suppose that the problem's notoriety had caused polarization among the members of the relevant disciplines (a widespread phenomenon in ideological competitions). This would represent a considerable enlargement of the "unwelcome mat" on which the outsider stands.
Suppose one were standing on such a mat. If nothing else, this could entail a more exacting scrutiny of his "credentials". But if one had held such things intellectually useless, he might not have garnered enough of them to deflate too many stuffed shirts...whose all-too-human accepting syntaxes are wont to exclude embarrassing truths from their computations. There may thus exist an atmosphere in which "credible" but overly ambitious theoreticians might feel encouraged to try a little quasi-plagiaristic sleight of pen. Of those who have bought so heavily into the system that this seems impossible to them. I must request that they spare me any lectures on its supporting dogma (I tend to be unsympathetic to dogma in general).
Academic credentials generally include things like advanced degrees, associates and references, past publications, former and current grants, fellowships, achievement awards, jobs in research facilities and universities, and so on. If laurels were strictly correlated with ability, the world of science and philosophy would topheavy with Newtons, Pasteurs, Gausses, and Kants. That this is not so is evident to anyone immune to hype. Unfortunately, to lack any such plumage can make one seem ragged and forlorn, a mere beggar at the gates of the mighty...and to no one so much as to the "mighty" themselves. If you've been to college, you know the score. Whoever has not seen it, has wanted not to see it.
Mr. Hoeflin points out that he has again changed the name of the group, this time to "The One-in-a-million Society". For my part, this seems rather less dignified than "The Noetic Society". However. in view or the fact that the new name has been given to The Encyclopedia of Associations and Omni Magazine, I will use both names in the heading.
Now we come to the part or Mr. Hoeflin's letter that requires a more detailed response. It was admittedly written before he had a chance to read the paper I wrote. I will quote it verbatim.
"I personally never heard of Newcomb's paradox until Chris Cole mentioned it. I don't feel sufficiently versed in probability theory to contribute any thing significant to the topic beyond what I briefly mentioned in one of my editorials - namely, that the problem seems to involve the interrelationship between action and knowledge, i.e., 'infinite' freedom of action versus 'infinite' knowledge. It may well be that, as in Heisenberg's Uncertainty Principle, the 'product' of these two factors is some constant, so that the greater the freedom, the less the knowledge must be, and the greater the knowledge the less the freedom must be. . . my own feeling was that the mechanism by which the Infinite Knower comes by his knowledge has to be spelled out better."
By any ordinary standards, these comments are quite well-put. However, my own background in philosophy leads me to remark that a great deal of philosophical terminology is either too nebulous, or overly complex and viciously circular in its abstrusities. One is often served a large portion of cotton candy or pretzels, when his appetite is geared to more substantial fare. Fortunately for those on stricter intellectual diets, the CTMU provides an appropriate conversion of terminology.
In the CTMU (Computation-Theoretic Model of the Universe), everything is given a computative construction. The necessity of this follows from the inability of the human mind to understand anything except by virtue of intellectual computation. Thus, terms like "knowledge", "freedom", and "action" must be made meaningful with respect to various classes of G-subautomata. In this case, we need go no farther than the elementary theory of cybernetics in order to clarify the relationships to which Mr. Hoeflin alludes.
Consider the cybernetic relationship between variety and constraint. "Variety" is that property of a set defined as the number of distinct elements it contains, regardless of their order of occurrence or degree of repetition. "Constraint" is a relation between two sets, defined as that by virtue of which the variety of a set under one set of conditions is less than the variety of a similar set under another set of conditions. Since, when one goes up, the other goes down, and vice versa, they are related by an informational invariant similar to that embodied in the Heisenberg uncertainty principle of quantum theory.
When the elements of a set are modeled as vectors, as they are in physics and the study of neural networks, they have components analogous to the dimensions of a Euclidian vectorspace. These may be used to define an upper limit on the variety of the set. Where the actual variety of the set is observed to be less than this limit, we may consider that number of components which, in the absence of constraint, would give the observed variety. This number of components is said to quantify the "degrees of freedom" of the set. Logically speaking, the addition to a vectorspace basis of an independent (orthogonal) dimension is the adjunction to the vectoral syntax of a base-space-inderivable, universally-quantified range of predicates. This range is a new degree of freedom relative to the structure, receptivity, and behavior of (vectorally-modeled) automata. With respect to the conserved total variety of an unconstrained set, its post-constraint degrees of freedom relate complementatively to degrees of control.
What is "knowledge", relative to a given acceptor F? Usually, something known is something recognized. Knowledge is thus defined on a combination of input, state transition, and acceptance. The input alphabet S of F has a variety equal to the number v = |S| of distinct symbols it contains. The set SN of input strings s, with variety ∞S0 (vI) (i = 0, 1, 2, ...), is not only limited with v, but is constrained by the M-automated algorithm d (q,s), each phase of which corresponds to one of a system of "goals" related within it. This system amounts to a hierarchy of constraints, each of which further reduces that variety of Sn which remains after the last phase of recognition. Knowledge may thus be categorized by levels of organization corresponding to the stratification of d. Randomly memorized trivia is low-level knowledge; highly organized, goal-relevant information is higher-level knowledge. But there exist higher kinds yet.
A simple paradigm is easy to provide. Suppose you have always lived in a labyrinthine enclosure, and that an algorithm exists by which you can always determine your location within it. The algorithm first tells you which half of the enclosure you are in. Once you know that, it tells you which half of that half you arc in, and so on until you know your exact position. At each step, knowledge is gained in the form of a further constraint on your whereabouts. Now, suppose that in the course of your explorations of this enclosure you discover something entirely new: a window. Looking through it, you see for the first time an "outer space" replete with planets, stars, and galaxies. You have gained a whole new range of knowledge; the primary constraint represented by the boundary of your enclosure has been suspended. Were you a logician or a topologist, you could even go on to construct "windows of abstraction" through which new dimensions could be glimpsed. The Newcomb transducer MN happens to have such a window glazed with empirical data - i.e., data from observations of the paranormal efficacy of Newcomb’s Demon.
Knowledge has one of two bearings on recognition. In its common form it is identical with constraint and narrows the variety of an algorithm's domain as information is gained. In the form taken by knowledge in The Resolution of Newcomb's Paradox, it represents a general extension of the accepting syntax, or equivalently, the suspension of a primary constraint. On one hand, we have knowledge as it is usually defined; on the other, we have a new parameter of knowledge amounting to a new degree of cognitive freedom. By the manner of its induction, this adjoined parameter is sufficient to effect the computative nesting of one transducer within another, and of both within an arbitrary mechanistic extension of standard reality.
Where "action" is considered synonymous with the output behavior of a transducer M, a vectoral representation of M's range of output promotes consideration of its degrees of behavioral freedom (relative to specific goals and conditions, freedom can often be absolutely quantified; here, it is instead considered as dependent on recognition). Algorithms, especially strategic ones, often mirror an external reality in which concrete objectives are defined. Such objectives, unlike victory in Newcomb's game, cannot always be achieved by means of a single action. In cases where action elicits a variable dynamic response critical to algorithmic progress, it can be considered a part of the algorithm itself. In this algorithmic externalization, the outer dynamic becomes part of the device in which the algorithm runs. Viewed in this light, "freedom of action" is seen to be constrained in the same way as computation. This means that where knowledge is restrictive, it does indeed limit (degrees of) freedom of action.
However, extensional knowledge (like that which our labyrinth-dweller found through the window) and transcendental knowledge (like his mental discovery of another dimension) do the opposite, and these kinds alone can resolve such paradoxical inconsistencies between logical and probabilistic dependence as that which figures in Newcomb' s paradox. So it is not strictly correct to identify the relationship between knowledge and freedom of action with that between constraint and variety. Rather, it is more accurate to say that the relationship of knowledge to freedom depends on the relevance of knowledge to constraint, where all of these terms are relativized to a coherent algorithm. Sometimes we have covariance like that mandated by the Heisenberg uncertainty principle, and sometimes not. One need not go too far afield to find cases in which knowledge constrains in order to promote a subsequent range of freedom, or where it frees and constrains at once.
The abstract organo-robotics of the Resolution aids precision.
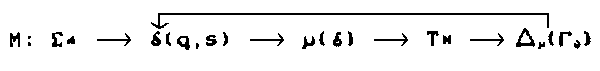
depicts a feedback loop in which the outward results of M’s output become parametric over d and thus in effect over m. The past behavior of M thus governs its future behavior by introducing, relaxing, or eliminating constraints within d (where d is defined as self-modificative on this basis). This may result in (M-recognized) degrees of freedom being lost or gained by TN.
Where knowledge constrains, frees, or transcends action, it is a predicate of action. Yet, where knowledge is actively computed, it is action…“action of higher type". It is thus pointless to speak of unstratified knowledge or action, "infinite" or not. Any attempt to do so will lead inevitably to logical contradictions by violations of type. Moreover, as "infinite" knowledge can signify a total absence of constraint in a partial set of parameters - the remaining parameters being constrained — infinity must itself be parameterized by specific G -subautomatonic predicates. The related complexities, though well in hand, exceed our present purposes and must therefore be deferred to a future discussion.
(The following annotated bibliography was sent to me by Martin Gardner. In view of the limited circulation and nonprofit status of Noesis, I assume that he would not object to our use of it. His own comments on the paradox may be sampled in the Mathematical Games Department of the July, 1973 issue of Scientific American, as well as in his books Knotted Doughnuts and aha! Gotchca (W. H. Freeman), and The Whys of a Philosophical Scrivenesr (Morrow). I will try to address some of these comments in a later issue.)