nov92

Noesis

The Journal of the Mega Society

Number 75

November 1992

EDITORIAL

Rick Rosner

5139 Balboa Blvd #303

Encino CA 91316-3430

(818) 986-9177

After several months of being caught up, I've fallen down again. Though I have many convincing excuses, the main reason is petulance at my laziness and lack of responsibility which drives me into a deeper shiftless funk.

________________________________

Kevin Langdon phoned me about his test, the LIGHT, which we reprinted in the October issue. He says that the small scale at which we printed it makes it hard to solve some of the problems. Also, he plans on publishing a new edition which may refine or eliminate some of the current questions. Troublesome problems might include 8, 10, 13, 20, 22, 26, 27, 28, 30, 34, 37, 38. He'll let us print his new edition, but only in a larger size.

________________________________

A bunch of good stuff has accumulated in the last couple of months. Leading off is:

LOTS OF E-MAIL

by Dean Inada, M.C. Price, Chris Cole, et al

Date: Mon, 7 Sep 92 02:15:02 -0700 From: dmi@peregrine.COM (Dean Inada)
To: chris Subject: Re: Newcomb's Daemon & Super-Rationalism Cc: price@peregrine

From: chris (Chris Cole) Subject: Re: blind watchmaker

To: dmi@peregrine.peregrine.com (Dean Inada) Date: Wed, 27 May 92 9:53:59 PDT Cc: price
In-Reply-To: <9205270323.AA24480@peregrine.COM>; from "Dean Inada" at May 26, 92 8:23 pm

> I think you cannot change the past; you can only change the future.
> You can only choose among futures which have non-zero amplitude.
> And you can only choose among pasts which have non-zero amplitude.

You are using "choose" in a funny sense -- which leads me to suspect you
want to talk about determinism versus free will. I am happy to talk about
that, which I feel is basically a semantic problem, but I think it is off the
subject of correlation versus causation. Cause-and-effect makes little sense
if you look on the universe as a giant wave function evolving in time; this is
because everything causes everything else. This is kind of a mystical view.
Fortunately, the universe appears to be governed by local laws, so it is
separable into objects, events, etc. Then it makes sense to say that
one event caused another, in the sense that if the universe did not
contain the prior event, it would not contain the subsequent event.

This dependence of causality on locality has the consequence that as
time goes on, the effects of a given cause are hard to determine.
Everything gets tangled. Then we can only speak of correlations.

> But any asymmetries in how often erasure occurs in +t vs. -t seems to be
> largely artifacts of the boundary conditions of your setup)

I agree that the apparent asymmetry between +t and -t is possibly an
effect of boundary conditions.

How the underlying time-symmetric laws of physics lead to the
asymmetrical cause-and-effect relationship has been discussed often.
Hawking talks about it and gives four explanations. I think the "real"
answer is unknown at this time.

Remember that I admit that I have no evidence for causality.

> What does a "change" to the future mean anyway, if not an ex-nihilo cause?
> And why must an ex-nihilo event imply the ability to change the past?
> or inability to change the future?

If you don't know what it means to change the future, I don't know how
to explain it to you. I certainly don't believe in ex-nihilo anything,
so I am not proposing them.

> If you can understand the laws by which a non-local causailty operated,
> why couldn't you take that into account in your decisions?

How would I determine which piece of the universe to look at? Of
course, if the non-local causality was approximately local in some way
(like limited in distance, or something), that might help.

One could argue that it's just my tough luck if I can't decide what to
do given the non-local laws of nature. This sounds right, but I am
worried that causality somehow implies locality, and that evidence
somehow implies causality. In other words, I am concerned that although
we can think about non-local theories, they are impossible to verify.
They are akin to metaphysics.

> One can do no better than to choose to do what seems less likely
> to be a mortal sin, (and it would be a less than ideal plan which
> depended criticaly on my exercising abilities which I lack)

This assumes you have a basis for assigning likelihood. Without
evidence, this is impossible. Christian existentialists figured out
that a being with infinite capacities is hard to gather evidence about.

Date: Wed, 27 May 92 15:20:01 -0700 From: dmi (Dean Inada)
To: chris, dmi@peregrine.peregrine.com Subject: Re: blind watchmaker Cc: price

> >          I think you cannot change the past; you can only change the future.
> > You can only choose among futures which have non-zero amplitude.
> > And you can only choose among pasts which have non-zero amplitude.
>
> You are using "choose" in a funny sense -- which leads me to suspect you
Well, I didn't know how you were using "change".
> want to talk about determinism versus free will. I am happy to talk about
> that, which I feel is basically a semantic problem, but I think it is off the
Indeed, I don't know you mean by "free will".
But if you wish to talk about it, I would probably try to see if your
statements about it in +t could also apply to -t.
> subject of correlation versus causation. Cause-and-effect makes little sense
> if you look on the universe as a giant wave function evolving in time; this is
> because everything causes everything else. This is kind of a mystical view.
> Fortunately, the universe appears to be governed by local laws, so it is
> separable into objects, events, etc. Then it makes sense to say that
> one event caused another, in the sense that if the universe did not
> contain the prior event, it would not contain the subsequent event.
Which is not strictly true, since there can be more that one prior event
which could lead to the same subsequent event, but as far as it goes,
can't it also be said that if the universe did not contain the
subsequent event, it would not contain the prior event?

> > But any asymmetries in how often erasure occurs in +t vs. -t seems to be
> > largely artifacts of the boundary conditions of your setup)
> I agree that the apparent asymmetry between +t and -t is possibly an
> effect of boundary conditions.
Perhaps a major (local) asymmetry in boundary conditions is the difference
between conditions at about - 10^10 years and + 10^10 years from now.
I might imagine that if you could set up an experiment arranging the + 10^10
boundary condititions to be like our - 10^10 boundary conditions,
you might see very similar things with just a sign change.
>
> How the underlying time-symmetric laws of physics lead to the
> asymmetrical cause-and-effect relationship has been discussed often.
It seems to be basicly a greater number of possible futures than pasts.
And the past seems to be highly anomolous in being much more highly
contstrained than one might usualy expect on average.
>
> > If you can understand the laws by which a non-local causailty operated,
> > why couldn't you take that into account in your decisions?
>
> How would I determine which piece of the universe to look at? Of
> course, if the non-local causality was approximately local in some way
> (like limited in distance, or something), that might help.
Even with locality, your backward light cone is already too big
to look at everything. And events outside your light-cone can still
influence events in your future light cone, so I don't see how
locality solves this problem eiher. In practice, we deal with
approximations to reality, and seem to get by.

> One could argue that it's just my tough luck if I can't decide what to
> do given the non-local laws of nature. This sounds right, but I am
> worried that causality somehow implies locality, and that evidence
> somehow implies causality. In other words, I am concerned that although
> we can think about non-local theories, they are impossible to verify.
> They are akin to metaphysics.
I haven't heard any convincing non-local theories either, but we
can certainly look for tachyons in particle chambers, or try to send
messages via wave function colapse, or send clocks around spinning
black holes or whatever.
And I think there are a number of (perhaps inelegant) ways in which
to have non-locality while preserving causality.

> This assumes you have a basis for assigning likelihood. Without
> evidence, this is impossible. Christian existentialists figured out
> that a being with infinite capacities is hard to gather evidence about.
A potentialy infinite universe can be hard to gather evidence about too.
(especialy without the possibility of direct interrogation :-)
but we muddle along anyway, and live with the possibility of error.

I don't know which of uncertainty or non-locality, or acausailty
I should accept, but it seems like Bells inequality implies one of them.
If you want to reject each of them, are you also rejecting Bells inequality?
Or the experiments which appear to confirm it?

From: chris (Chris Cole) Subject: Re: blind watchmaker
To: dmi (Dean Inada) Date: Wed, 27 May 92 23:34:24 PDT Cc: price
In-Reply-To: <9205272220.AA10978@peregrine.COM>; from "Dean Inada" at May 27, 92 3:20
...
> > How the underlying time-symmetric laws of physics lead to the
> > asymmetrical cause-and-effect relationship has been discussed often.
> It seems to be basicly a greater number of possible futures than pasts.
> And the past seems to be highly anomolous in being much more highly
> contstrained than one might usualy expect on average.

Agreed, there is something fundamental we do not understand yet.

> Even with locality, your backward light cone is already too big
> to look at everything. And events outside your light-cone can still
> influence events in your future light cone, so I don't see how
> locality solves this problem eiher. In practice, we deal with
> approximations to reality, and seem to get by.

OK, but its a lot easier to approximate with local causality than without;
it might even be infeasible without local causality to approximate.

> can certainly look for tachyons in particle chambers, or try to send
> messages via wave function colapse, or send clocks around spinning
> black holes or whatever.
> And I think there are a number of (perhaps inelegant) ways in which
> to have non-locality while preserving causality.

I'm not so sure. Since you brought it up, let's talk about another
spooky thing: time travel. I think the arguments are analogous, but I
haven't thought it out in the case of non-local theories.

We know that time travel leads to kill-your-grandfather causality
paradoxes. Now, people have proposed models of the universe that solved
the equations of general relativity that seemed to include time travel.
Godel was the first; Guth recently. As far as I am aware, all such
theories have been shot down on closer examination. They either
required more time or more mass than the universe has. Kip Thorne has
stated that the universe protects itself against time travel. As you
might imagine, this teleological bias drives me crazy ... but anyway,
the point is that you can't have a solution that has a causality
paradox. Why? Because you believe in causality more than you believe
in the theory. If the theory allows causality paradoxes, then the
theory must be wrong. Is this a violation of scientific objectivity?
No, because science itself assumes causality. If there is no causality,
there is no evidence; if no evidence, no science. Therefore, I can have
unshakeable faith in causality -- I'm sure no one will ever prove me
wrong!

Now, take non-local theories (like signalling with wave function
collapse, or whatever). Since there is no limit to how far apart the
two decay products could be, this implies that we can cause
instantaneous state changes over unlimited distances. Therefore, it is
impossible for me to predict the value of my local state function one
second from now without knowing everything that is going on in the
universe. This effectively destroys causality. Thus, I simply reject
non-local theories as too awful to contemplate.

You might say -- wait a minute! You can't reject a theory like that.
But suppose a theory allows for logical contradictions. Surely we all
agree that such a theory is not possible. It's not even really a
theory, since it makes no definite predictions. Well, neither does the
non-local theory (or the time travel theory). The universe simply can't
work that way.

> I don't know which of uncertainty or non-locality, or acausailty
> I should accept, but it seems like Bells inequality implies one of them.
> If you want to reject each of them, are you also rejecting Bells inequality?
> Or the experiments which appear to confirm it?

My position is that we don't understand enough about what time is to
answer questions like this yet. Sure, if you put a gun to my head and
forced me to choose between locality, causality or determinism, I would
reluctantly throw out determinism. I can live with local, causal
non-determinism because I can plan my life to avoid the uncertainties.
And I agree that Bell's Theorem makes it look pretty bleak for
determinism (although of course this is really built in to the
assumptions of quantum mechanics -- the whole idea of representing
particles with field theory). But then particles were an absurd idea
anyway, so maybe determinism is just a chimera. At any rate, I don't
have a gun to my head, so I can maintain a comfortable agnosticism.

Hopefully, there'll be time to sort things out.

Date: 28 May 92 02:39:33 EDT From: Michael Clive Price <100034.3077@CompuServe.COM>
To: Dean Inada <dmi@Peregrine.com>, Chris Cole <chris@peregrine.COM> Subject: Re: Various

>> My third effort for the half-planar woods is 6.458912.. miles.
4th effort: 1 + 7pi/6 + sqrt(3) = 6.39724.. (3rd effort = jebat natyr)

> I think you cannot change the past; you can only change the future.
Past(s) and future(s) are both immutable according to Newton, Maxwell,
Einstein and Everett, since all have time-symmetric deterministic
equations. I would rather say that the distinction between past and
future is that we remember the past but 'cause' the future, the arrow of
time being a consequence of the increase of entropy / boundary
conditions. (see later)

> Actually, Dean and I will be at the Artificial Life conference in
> Santa Fe in two weeks...
Sounds quite interesting, I look forward to the report.

> I assume you are interested in the contract idea. Correct?
Yup.

> You don't like that nature uses amplitudes instead of probabilities?
The probability of an event must be the sum of the probabilities of the
alternative sub-events. Since squares of 'alternative' amplitudes don't
add they can't be alternatives. eg the electron doesn't choose between
which slits to pass through - it passes through both (according to many
worlds).

> My position is this: don't form metaphysics based on known incomplete
> physics. We know that the Standard Model (U(1)xS(2)xS(3)) does not
> include enough particles to be correct. We know that GUT (SU(5)) has
> similar problems.
I agree, we know that U(1)xSU(2)xSU(3) must be embedded in some more
complex group and that this is not SU(5). But this is no different from
the state of physics at previous times, where physicists continually
refine their equations/models. BUT for each set of incomplete physics in
the past there has been a corresponding set of metaphysics that provides
a model - in fact we often identify the two because the models are so
compelling
eg
Newton = point particles + action-at-a-distance
Maxwell = fields, ether and point particles
Einstein = curved space-time/geometrodynamics
Each theory of nature supplied its own interpretation. It would be a
mistake to suppose that superstrings, Kaluza-Klein or whatever are going
to rescue physics from the metaphysical hole it has fallen down. All the
mainstream directions at the edges of physics (superstrings, Kaluza-Klein
or whatever) are WITHIN the framework of quantum field theory. It is
very noticable how out-on-a-limb most attempts to resolve the paradoxes
of QM are.

The Everett model is the natural (= coherent) interpretation of quantum
theory. Advances in physics are not going to invalidate Everett, but
rather refine and extend his many-worlds picture of the universe. Just
as the Newtonian billard-ball model is still useful in many mechanical
analyses or Maxwell's equations are still used in waveguide theory.

> It is therefore sensible to talk about quantum gravity involving
> quantizing geometry (i.e., space-time). This is all I mean about
> granularity at the Planck scale..... it is possible that all of
> physics is geometry.
Agreed. Superstrings look like a good candidate for quantum
geometrodynamics.

> So, what is my position? ... I don't have to choose between
> Copenhagen, Everett, hidden variable, etc.
Except that with cryonics and many-worlds you are certain of revival;
Objectively:
Those worlds in which have you suffer 'meltdown' (eg thermonuclear
holocaust or economic collapse) you simply don't wake up in. Those
worlds which develop UIMs and prosperity you are revived in.
Subjectively:
You experience revival.
Moral:
Many-worlds is not entirely some metaphysical irrelevance to life.

> How the underlying time-symmetric laws of physics lead to the
> asymmetrical cause-and-effect relationship has been discussed often.
> Hawking talks about it and gives four explanations. I think the
> "real" answer is unknown at this time.
I think people make too much work of the matter. Cause-and-effect equals
the flow of time, comes from the slide of universe from a low entropy
state to a higher entropy state, comes from inflation just after the Big
Bang. Inflation explains the flatness of the universe, its huge size and
age etc. Where's the mystery?

> You are using "choose" in a funny sense -- which leads me to suspect
> you want to talk about determinism versus free will. I am happy to
> talk about that, which I feel is basically a semantic problem,
Agreed
> but I think it is off the subject of correlation versus causation.
> Cause-and-effect makes little sense if you look on the universe as
> a giant wave function evolving in time; this is because everything
> causes everything else. This is kind of a mystical view.
???? Surely not. Since the QM is locally deterministic it's mystical (=
illogical) to believe in anything else?

> Fortunately, the universe appears to be governed by local laws, so it
> is separable into objects, events, etc.
Agreed. Very handy. And a consequence of the speed of light, which
forbids non-locality.

Date: 11 Jun 92 18:05:00 EDT From: Michael Clive Price <100034.3077@CompuServe.COM>
To: Dean Inada <dmi@Peregrine.com>, Chris Cole <chris@peregrine.COM>
Subject: Re: micro-symmetry ==> macro-asymmetry

>>           BTW, Dean, you still haven't answered my question about
>>           what you believe/don't believe QM means.
> I believe I am happy with the many worlds interpretation.
> Or is this a deeper question about belief?
No, just curious. Many-worldists are a fairly rare breed, although I
understand that it's the most popular interpretation amongst quantum
gravitists (according to a straw poll at an Oxford QG symposium a few
years back).

> I'm not sure what my subjective impression of having
> my corpsicle revived by the flip of Shrodinger's cat would be,
> But then, I also get confused about what it would be like
> to download myself into a bunch of classical robots and then
> to kill half of us.
Yeah, I worry about that as well.

>>           The Everett interpretation is able to explain Bell's theorem,
>>           but within a local and deterministic model. Bell never
> Is that our old or new sense of the word deterministic?
Both, since Everett has past <==> future, like classical mechanics. Or
perhaps I should say, past(s) <==> future(s)

>>           >From the definitions and detailed balancing it follows that
>>           (proof on request):
>>                  (2nd Law of Thermodynamics)
>   Yes, I'd like to see the proof,
>   There's usualy a boundary condition introduced somewhere
>   at this point.
Okay, what follows is Everett's general proof. For some reason it seems
easier to prove it for the more general case where detailed balancing
doesn't hold and then specialise it to where detailed balancing (read:
unitarity) does hold. Everett also covered the continuous case, but,
since I can't draw integral signs very easily, I shan't. Can't improve
on the elegance of the original, so here it is from Everett's "Theory of
the Universal Wave Function" doctoral thesis: a couple of lemmas followed
by the 2nd Law.
------------------ Lemmas 1 & 2 ----------------------------------
Appendix I,
#2. Convex function inequalities

LEMMA 1.

This property is usually taken as the definition of a convex function,
but follows from the fact that the second derivative of x ln x is
positive for all positive x, which is the elementary notion of convexity.
There is an immediate corollary for the continuous case: [continuous
proof deleted]

We can now derive a more general and very useful inequality from Lemma 1:

LEMMA 2.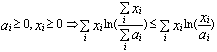
We also mention the analogous result for the continuous case: [continuous
proof deleted]
------------------------ 2nd Law --------------------------
Appendix I,
#4 Montone decrease of information for stochastic processes

We consider a sequence of transition-probability matrices,



and a sequence of measures a >= 0 having the property that

[as far as I can see the "a" measure is just an arbitrarily chosen set of
numbers that we can dispense with in the unitarity-true case - but we
need them to generate an entropy-like thing in the more speculative case
where unitarity is not true]

We further suppose that we have a sequence of probability distributions

For each of these probability distributions the relative information

  (relative to the    measure) is defined
   [generalised entropy,]

under these circumstances we have the following theorem:

THEOREM.    [i.e., ]

Proof: Simply substitute the two lemmae above into the equation.

------------------- end of excerpt -------------------------------
We can recover the Shannon definition of entropy

in the doubly-stochastic case (= unitarity = CPT invarinace) by chosing
the unit relative measure, a = 1, which is a stationary measure, we can
remove a from all the above formulae and get:

[i.e., ]===> 2nd Law of Thermodynamics

By basing the proof of the 2nd Law on the informational definition of
entropy (from which it is quite easy to recover S = k ln W and dE = Tds +
dW) the proof of the 2nd Law becomes insensitive to the fine details of
physics, dependent only on unitarity. Thus:

unitarity ==> entropy ==> arrow of time

Hence the arrow of time always points away from entropy minima towards
maxima. The fact that we live in a reversible universe and have an arrow
of time tells me that the past has lower entropy than the future. Is this
the boundary condition you were looking for Dean?

Too tired to think straight. Sorry if the proof is a little opaque and
messy (duplicated indices and all that). It blew my mind when I first
encountered it. Speak to you both later.

MCP

From: chris (Chris Cole) Subject: Re: The Tangled Web

To: price Date: Sat, 9 May 92 10:38:33 PDT Cc: dmi (Dean Inada)

Date: 21 May 92 17:16:43 EDT From: Michael Clive Price <100034.3077@CompuServe.COM>
To: Chris Cole <chris@peregrine.COM>, Dean Inada <dmi@Peregrine.com>
Subject: Re: blind watchmaker

>> Also, Penrose's nonsense notwithstanding, I understand there does
>> exist a thought experiment in which an Everett turing machine might
>> be able to beat any Classical or Copenhagen turing machine through
>> quantum parallelism.
> I would like a reference to this.

Try
     "Quantum theory, the Church-Turing principle and the universal
      quantum computer", by David Deutsch, Proceedings of the Royal
      Society London. A 400, 97-117(1985).
But...
Unfortunately the "Everett turing machine" can't beat the the others in
any real-world situation. Deutsch shows that a quantum computer fails
sufficiently often so that the average time taken to perform any
calculation using quantum parallelism must exceed the conventional
"Copenhagen" or serial computation. His proof neglects to cover the case
of the reversible quantum computer which dosen't suffer from this defect.
But in any case the types of problems amenable to cracking (by any form
of quantum computer) are too restricted to be useful in most "real-world"
situations.

I had an e-mail dialogue with Deustch about this, which I can forward
onto you if you're interested.

> The idea that quantum effects are truly random (versus
> computationally random) has not been proven, yes?

Insofar as any physical theory can be proved quantum theory has passed the
tests with flying colours. Everett, by completing the philosophical basis
of QM (i.e. removing the vitalistic element of observer-triggered
wavefunction collapse), showed that whilst QM was an objectively
deterministic theory it was subjectively random. So I would say that
quantum effects are truly subjectively random, even if objectively
deterministic.

BTW I know that Feynman regarded his sum over histories approach as side
stepping the wavefunction collapse problem, which he described as a
fiction. This approach requires non-additive probabilities, which I
regard as mathematically impossible. Given a choice of the physically
implausible (many-worlds) or the mathematically impossible I have to
choose the former. Do you know what Feynman thought of many-worlds?

-MCP

PS the easy answer I saw to the half-planar woods was the 1+2pi solution.
I shall carry on looking for a harder solution.

From: chris (Chris Cole) Subject: Re: blind watchmaker
To: elroy!ames!mimsy!uunet!compuserve!100034.3077 (Michael Clive Price)
Date: Fri, 22 May 92 15:51:29 PDT Cc: dmi (Dean Inada)

Thanks, I'll get this paper. By the way, Dean, you never did respond to
my question about the origin of your claim that local causality is known
to be wrong.

> I had an e-mail dialogue with Deustch about this, which I can forward
> onto you if you're interested.

If it's not too much trouble, I would be very interested in this.

> Insofar as any physical theory can be proved quantum theory has passed the
> tests with flying colours. Everett, by completing the philosophical basis
> of QM (i.e. removing the vitalistic element of observer-triggered
> wavefunction collapse), showed that whilst QM was an objectively
> deterministic theory it was subjectively random. So I would say that
> quantum effects are truly subjectively random, even if objectively
> deterministic.

Two objections:
1. Everett might be wrong. I am still perturbed by Bohr's comment that
QM in 4 dimensions is like C(lassical)M in five. What is spin, anyway?
2. Quantum random STILL could be the same as computational random, via
something like CTMU, Fredkin, etc.

> BTW I know that Feynman regarded his sum over histories approach as side
> stepping the wavefunction collapse problem, which he described as a
> fiction. This approach requires non-additive probabilities, which I
> regard as mathematically impossible. Given a choice of the physically
> implausible (many-worlds) or the mathematically impossible I have to
> choose the former. Do you know what Feynman thought of many-worlds?

You are going way too fast for me here. Why is many-worlds any different
from many-histories (a term Gell-Mann prefers -- and I agree)?

From: chris (Chris Cole) Subject: Re: blind watchmaker
To: dmi@peregrine.peregrine.com (Dean Inada) Date: Fri, 22 May 92 15:55:25 PDT Cc: price

> PS the easy answer I saw to the half-planar woods was the 1+2pi solution.
> I shall carry on looking for a harder solution.
> Hmm, it seems that the 1+2pi answer is just so attractive that
> one tends not to think of looking for improvements.

Yes, that of course is what makes it a good problem.

> (Might 1+2pi be the solution to the question of minimizing the
> expected value of the path to the road? That may be another
> possible variant of the puzzle)

Are you saying it might be, or that you think it is, and if so, why?

Re: half-planar woods
Aha! Down to 2+pi3/2 now.
2 1/2
And f(x) = ( 1/(1+i) + ix )

Right, now for the hypercubes...

PS I'll send the stuff about Deutsch a bit later.

From: chris (Chris Cole) Subject: Re: blind watchmaker
To: dmi (Dean Inada) Date: Sat, 23 May 92 0:58:52 PDT Cc: price

> Is that what you asked, I must have misunderstood.
> Anyway, doesn't the Bell inequality show that the predictions of any
> local hidden-variables theory were inconsistent with those of QM.
> (although there may still be some loopholes in the experiments to confirm it,
> for example, the particles could still have "conspired" before
> hand with the measuring aparatus, and, knowing on which axis their
> spin was going to be measured, adjusted their correlations accordingly)

Don't you think it's a bit much to claim that just because wave
functions collapse, local causality is out the window? Isn't it more
likely that wave function collapse does not correspond to a physical
process. This, I gather, is what Everett is getting at. I am not sure
though. At any rate, like Hume, I am much more attracted to the idea
that wave function collapse is non-physical than that local causality is
violated.

>              1. Everett might be wrong. I am still perturbed by Bohr's comment that
> Which is what makes the possibility of an experimental test to interesting.
>              QM in 4 dimensions is like C(lassical)M in five. What is spin, anyway?
> What is this? Anything like the Kaluza-Klein unified field theorys?

This is an obscure statement by Bohr that I am still trying to
understand and track down. It may be related to Kaluza-Klein, but I am
not sure.

>              2. Quantum random STILL could be the same as computational random, via
>              something like CTMU, Fredkin, etc.
> Wouldn't this be a Hidden Variable theory?

I don't think so. If the universe is a computer -- a cellular automaton
with finitely many cells -- then computational randomness IS physical
randomness, and the mathematical ideal of computational randomness can
never be purely attained, but only more or less approximated. This is
what most physicists envision the ultimate merger of quantum mechanics
and gravitation (i.e., geometry) will yield. They might be wrong, of
course.

>              You are going way too fast for me here. Why is many-worlds any different
>              from many-histories (a term Gell-Mann prefers -- and I agree)?
> Is it different? I thought they were two names for same treatment,
> and that both were synonymous with Everett's interpretation.

I think that too. But Mike threw me for a loop here. What is this
about non-additive probabilities?

Date: 24 May 92 18:58:25 EDT From: Michael Clive Price <100034.3077@CompuServe.COM>
To: Chris Cole <chris@peregrine.COM>, Dean Inada <dmi@Peregrine.com> Subject: Various

Re: Noetic problems
My third effort for the half-planar woods is 6.458912.. miles. Definitely
a VERY good problem!

Re: quantun gravity and granularity of space
>> What is it that physicists think quantum gravity will yield?
> My sense is that "they" (and I include myself in this group) expect
> to find that there are finitely many cells of the Planck length...
I have never seen any evidence for space being granular (if that's what
you referring to). Even if space-time becomes frothy on the Planck scale
(which I think it will) that's not the same as granular. But perhaps you
use the word in a different sense....

Re: many-histories versus many-worlds
>>           You are going way too fast for me here. Why is many-worlds any
>>      different from many-histories (a term Gell-Mann prefers -- and
>>      I agree)?
> Is it different? I thought they were two names for same treatment,
> and that both were synonymous with Everett's interpretation.

I guess we'll have to ask Gell-mann that. I know that Gell-Mann doesn't
believe in many-futures, which is a consequence on many-worlds. But he
hasn't published his own many-histories variant (as far as I know), so we
don't know what he means by this.

To me it looks like:

Everett => many-worlds => many-histories and many-futures.

Gell-Mann seems to be trying to separate the unseparable.

> What is this about non-additive probabilities?

In Feynman's sum-over-histories approach objects are treated as classical
point entities that take all possible paths. Final states are regarded
as being the sum of all intermediate states. But the probability of a
final state is not the sum of the probabilities of the intermediate
states. (I know this is elementary to us, but I want to explain my
terminology). If probability is defined via relative frequencies of
events then this is simply not logically possible.

In the Everett many-worlds approach the fundamental objects of existence
are not point particles but the wave function itself. The wave function,
instead of just mathematically modelling reality, is treated as *being*
physically real, and therefore does not collapse. In the double slit
experiment the electron is not viewed as going through one slit or the
other, in particle fashion. Instead the wave function passes through
*both* slits and the paradox of non-additive probabilities is removed.

> 1. Everett might be wrong.

The Everett approach has the merit of being determinstic, locally causal
and treats observers in a reductionist fashion. Subjective probability
emerges from the formalism of the theory, rather than being built into
the axioms.

No one has constructed a relativistic hidden-variables theory.
Non-relativistic hidden variable theories are all either non-causal or
non-local. They are wishful pie-in-the-sky attempts to deny the
admittedly unsettling consquences of quantum theory. Copenhagenism is
not a scientific theory since it treats observers in a non-reductionistic
fashion, having to invoke them to collapse wavefunctions. Is a frog an
observer? Or an ant?

I believe that it's a straight choice between Everett and Hidden
Variables. It's always possible that a more refined theory (hidden
variables) will replace quantum theory. But many-worlds is such a
fundamental aspect of quantum theory that I'm sure it will be present in
whatever theory supersedes it. Just as planets still follow Keplerian
ellipses although classical physics is only an approximation.

MCP

From: chris (Chris Cole) Subject: Re: Various
To: elroy!ames!mimsy!uunet!compuserve!100034.3077 (Michael Clive Price)
Date: Tue, 26 May 92 17:49:42 PDT Cc: dmi (Dean Inada)

> as being the sum of all intermediate states. But the probability of a
> final state is not the sum of the probabilities of the intermediate
> states. (I know this is elementary to us, but I want to explain my
> terminology). If probability is defined via relative frequencies of
> events then this is simply not logically possible.

Well, the sum of the AMPLITUDE of the final state is the sum of the
AMPLITUDES of the intermediate states. Is this what you are objecting
to? You don't like that nature uses amplitudes instead of
probabilities? (But see below).
...
> I believe that it's a straight choice between Everett and Hidden
> Variables. It's always possible that a more refined theory (hidden
> variables) will replace quantum theory. But many-worlds is such a
> fundamental aspect of quantum theory that I'm sure it will be present in
> whatever theory supersedes it. Just as planets still follow Keplerian
> ellipses although classical physics is only an approximation.

My position is this: don't form metaphysics based on known incomplete
physics. We know that the Standard Model (U(1)xS(2)xS(3)) does not include
enough particles to be correct. We know that GUT (SU(5)) has similar problems.
They are discussed because they are probably good approximations for
certain temperature ranges after spontaneous symmetry breaking.

We know that the only theories that have worked out are renormalizable
theories. This seems to indicate that such theories are embeddable in
some way in a theory of energy (=mass). Such a theory would be, of
course, be quantum gravity.

General relativity shows that the effects of mass are exactly equivalent
to the effects of geometry. It is therefore sensible to talk about
quantum gravity involving quantizing geometry (i.e., space-time).
This is all I mean about granularity at the Planck scale.

Kaluza-Klein shows that all conventional forces arise from gravity
(=geometry) in higher dimensions projected via collapse of some
dimensions onto fewer dimensions. Therefore, it is possible that all of
physics is geometry.

Superstrings are the only known candidate for a geometrical model that
has enough particles to be real and that is renormalizable. We don't
know much about the solutions to the equations of superstrings.

So, what is my position? All I know is that I know nothing. I don't
have to choose between Copenhagen, Everett, hidden variable, etc.
I don't think any of them are correct. My position is the same as,
perhaps, Maxwell's was when he calculated the spectrum of radiation from
a black body. "Hmm. Infinity can't be right. There must be something
wrong with my basic assumptions." The part I hope to avoid is the rest
of Maxwell's hypothetical conclusion: "I'll probably die before I figure
it out."

From: chris (Chris Cole) Subject: Re: blind watchmaker

To: dmi@peregrine.peregrine.com (Dean Inada) Date: Tue, 26 May 92 18:03:52 PDT Cc: price

> Playing devil's advocate, why are you so attatched to causality?
> All we have are correlations beteen events, (and P(A|B) does not have
> to equal P(B|A) (in fact they differ by P(A)/P(B)))
> and a theory that predicts when and how strongly events will be correlated.
> Why do you need anything more than the statement that, under a given theory,
> for the given conditions, A is a good/poor predictor of B or vice versa?

I think you cannot change the past; you can only change the future.
This is another way of saying that nothing happens without a cause.
Notice that I also am attached to local causality. This prevents
"spooky action at a distance." Without this, it is impossible to decide
what to do next. Sort of like Christian existentialism -- since you
can't know God's plan, anything you do could be a mortal sin.

What evidence do I have for causality? Hume answered that: none. So
why do I assume it? Why ask why?

A REVIEW BY M. C. PRICE

The full reference is 'Cauchy problem in spacetimes with closed timelike

curves', Physical Review D Vol 42, #6, September 1990, by J Friedman, MS

Morris, ID Novikov, F Echeverria, G Klinkhammer, KP Thorne and U

Yurtsever.

The article builds on some earlier work done on the possibility of

constructing a "time-machine" via wormholes connecting different regions

of space-time. You construct a wormhole (this is the hard part of the

recipe!), placing the usual obligatory, imaginary clocks at both ends.

Accelerate one end away to relativistic speeds so that it time dilates.

Then bring it back. If a traveller enters the wormhole at the

gone-away-and-come-back end he reappears out of the stayed-at-home end in

the past. The amount that the traveller goes back in time is the

difference in the clock readings.

Now imagine that the wormhole is connecting two of the pockets of a

pool table. So knocking a ball down one the pockets causes it to

reappear out of the other, at an earlier time. A paradox occurs when the

path of the ball is planned so that it collides with an earlier copy of

itself, deflecting the earlier ball from the path necessary for the later

ball to collide with it to exist. This is an impossible state of affairs

since the ball must travel on a well defined path (even if it does loop

back and forth through spacetime). What the article claims is that for

every paradoxical path there is another non-paradoxical path, with the

same *starting* path for the ball. Sometimes there are multiple

non-paradoxical paths (we'll come back to this later). If you plotted a

causality-violating path and sent your ball off towards the pocket then

as the ball approached the "entry" pocket a copy of itself would emerge

from the "exit" pocket BUT on a slightly different path than you had

calculated. Just sufficiently different so that, instead of knocking the

earlier version completely off course and missing the "entry" hole, it

has a glancing collision with its earlier self. The deflected earlier

ball now enters the "entry" pocket on a slightly altered path, which

accounts for the slightly different path that the later ball had taken on

exit from the other pocket. Thus the paradox has been resolved and

causality saved.

Whilst the authors claim to have proved this only for the elastic

collisions of a time-travelling ball with itself, they are hopeful that

it can be extended to more complex situations to remove more complex

paradoxes. It's fun to speculate on how time-travel paradoxes can be

averted by this mechanism [this is my own example]:

Suppose someone starts construction of a time machine, intent on

murdering their grandfather. Instead of appearing back in his

grandfather's time an older version of the traveller appears to the

younger, homicidal traveller and persuades him to abort the original

mission and instead go and use the time machine to stop the murder (by

talking his younger self out of it....). Presumably the older traveller

would have no problem persuading the younger version to change his

mission objectives, since he has memories of the encounter and

understands his earlier self very well.

The trouble with dreaming up these escape-from-paradox scenarios is that,

generally speaking, there are too many solutions (i.e. more than one) to

each potential paradox. The question arises, how does the universe

'choose' between the different resolutions? This is a problem in

classical, Newtonian physics, where balls (and atoms) are expected to

follow a single path. However in quantum theory you are allowed to

consider all the possible paths, via the Feynman sum-over-histories or

path-integral approach, which removes all ambiguities. This is the

solution proposed by the article. All possible configurations contribute

to the Feynman integral. The authors invite the reader to consider the

implications of this with regards to many-worlds!

-------------End of review-------------

Well, that's my version of the article. The conclusions I draw from it

are:

o There's no logical reason why we can't travel through time,

although the physical possibilities have yet to be demonstrated.

eg can we construct wormholes, rotating massive cylinders etc?

o We won't be able to change history.

o The mechanism that prevents the altering of history is the

presence of time travellers, either ourselves or others. They can

always pop up where least expected, with their behaviour generating

the conditions necessary for their own existence.

Nobody expects the .... the time traveller?

As for why we see no time travellers (to answer an unasked question). I

think that this is probably because the time machine can't move through

time. Of the three proposed mechanisms for time travel (spinning

blackholes, rotating cylinders and wormholes) each one only permits

travel over the life-time of the machine, which itself doesn't travel

through time. So we never get to photograph dinosaurs (sob!) unless we find a

time-machine that's been operating for 65million+ years. And similarly

our descendants (and ouselves!) can not come and visit us until we get

some time machines built ourselves.

M. C. Price

WHY WE NEED A SHORT FORM TEST

>From Arthur Watson via Kveld Hvatum:

...you may use the quote as well as my name and path, provided you do at

least the following editing to encapsulate the context, raise the

grammaticality, and lower the fatuousness to render it more suitable for

publication:

"Since I'm trying to finish my dissertation while holding a

fulltime job, I won't have a lot of free time in the next few

months, but I'd like to join societies that are convenient

(no 150-hour test) and have interesting journals. My

profession is computer science, but I have varied interests.

I got 760V 800Q 800A on the GRE general in 1985, and had a

780V 780M on the SAT in 1982 -- is this sufficient to get

into anything beyond Mensa?"

GREAT REWARDS FOR PROBLEM SOLVERS

FROM THE INTERNET

Great rewards are available to problem solvers worldwide! Here is a

list of math problems with $6800 in prizes!

If you are the first person to answer one of these questions, you get

the prize! Warning: The poser of each question is the sole and final

arbiter of what constitutes a completely correct solution, who is the

first to solve it, how much money a putative solution deserves, and all

other terms of the offer. The wording of the problems given here

is due to me, and the wording preferred by the problem posers may differ.

If you have ideas for one or more of these problems, you can send me

mail at greg@math.berkeley.edu. If the ideas are interesting and

especially if you crack one of the problems, I will try to get you

in touch with the relevant problem poser or posers.

You may conclude that problems with a large prize are impossible.

Some of them might be, but others have been solved. For example,

Walter Rudin offered $1000 for a solution to the question: Is there a

complex analytic function f from the open unit disk in the complex

plane to itself such that the image under f of every radius of the disk

has infinite length? The answer was recently provided by

Jean Bourgain of IHES. Unfortunately, I do not know it myself.

If you have your own math problem (or problems) with a prize attached,

please contact me. New contributions are always welcome. I can't

promise that I will include your problem in my list, but I will give it

serious attention.

The problems are listed by the size of the award, with the person

offering the prize and the amount wagered for a completely correct

solution. In the future there may be problems with a non-monetary

prize like a bottle of wine, a live goose, or tickets to the opera, as

well as problems for which the prize depends on the answer to the

question, for example $5000 for a yes and three lemons for a no. All

problems so far offer the same prize independent of the answer to the

question.

And now, the problems!

----------------------------------------------------------------------------

John Conway: $1000. The thrackle problem

A thrackle is a graph drawn in the plane with straight or curvy edges

in such a way that any two edges either cross each other exactly once

or share one endpoint, but not both. No other kinds of incidence

between edges or vertices or self-intersections of an edge are

allowed. Is there a thrackle with more edges than vertices?

Ron Graham: $1000. Monochromatic arithmetic progressions

Does every 2-coloring of the integers from 1 to 2^2^...^2 (k times)

have a monochromatic arithmetic progression of length k?

David Gale: $500. Decimal expansions of powers of 2

Are there infinitely many positive integers n such that 2^n

does not contain a 7 in its decimal expansion?

Ron Graham: $500. Triangular houses for worms

What is the shortest curve (not necessarily closed) that does not

fit in an equilateral triangle with unit sides?

Ron Graham: $500. 2n choose n relatively prime to 105

Are there infinitely many positive integers n such that 2n choose n

is divisible by neither 3,5, nor 7?

David Gale: $200. 3D Chomp

In the game of Chomp, two players alternate stating triples of

non-negative integers, and once a triple (a,b,c) is named, then for

ever after neither player can name a triple (d,e,f) with d>=a, e>=b,

and f>=c. A player who names (0,0,0) loses. Does the first player

have a winning strategy?

Greg Kuperberg: $100. Algebraic knotted tori

What is the minimum possible degree of a real polynomial equation in

three real variables whose solution set is a knotted torus?

Paul Erdos, the Hungarian problem solver extraordinaire, has offered

money for so many problems that I have decided to separate them from

the rest of my list. This posting is a partial list of Erdos prize

problems. At least $9050, and perhaps as much as $34100, in prizes,

are here for the taking!

Many of these problems were formulated jointly by Erdos and other

mathematicians. However, Erdos is the purser of all of the problems.

As I have mentioned before, the purser is the final judge and arbiter

of prize-winning solutions to each of the problems. The

award for a problem only goes to the person who solves it first,

and the purser is the arbiter of that too. I have given

my own description of each problem, but I am not responsible

for the consequences of mistakes or misleading wording in my

formulation.

If you are getting somewhere one of the problems, or if you plan

to try, you can contact me at greg@math.berkeley.edu. Please

contact me if you know of other Erdos prize porblems.

The problems listed here are from two sources:

T = A Tribute to Paul Erdos, Cambridge University Press, 1990, pp. 467-477.

P = Paths, Flows, and VLSI Layout, Springer-Verlag, 1980, pp. 35-45

The problems are labeled by their source and number in the reference.

In addition, problems in the first reference are labeled by topic:

N = Number theory

C = Combinatorics and graph theory

G = Geometry

----------------------------------------------------------------------------

$3000. (T3N) Divergence implies arithmetic progressions

If the sum of the reciprocals of a set of positive integers is

infinite, must the set contain arbitrarily long finite arithmetic

progressions?

$1000. (T2N) Unavoidable sets of congruences

A set of congruences n = a_1 mod b_1, n = a_2 mod b_2,... is

unavoidable if each n satisfies at least one of them. Is there an N such

that every unavoidable set of congruences either has two equal moduli

b_i and b_j or some modulus b_i less than N?

$1000. (T1C) Three-petal sunflowers

Is there an integer C such that among C^n sets with n elements, there

are always three whose mutual intersection is the same as each pairwise

intersection? (Problem P2 is the same, except that Erdos asks about

k-petal sunflowers for every k but then says he would be satisfied with

k=3.)

$500. (T7N) Asymptotic bases of order 2 (I)

Consider an infinite set of positive integers such that every

sufficiently large integer is the sum of two members of the set. Can

there be an N such that no positive integer is the sum of two members

of the set in more than N ways?

$500. (T8N) Asymptotic bases of order 2 (II)

In the context of the previous problem, let f(n) be the

number of ways that n is the sum of two members of the set.

Can f(n)/log(n) converge to a finite number as n goes to infinity?

$500. (T9N) Evenly distributed two-colorings

Given a black-white coloring of the positive integers, let A(n,k) be

the number of blacks minus the number of whites among the first n

multiples of k. Can the range of A be bounded on both sides?

$500. (T4C) Friendly collections of half-sized subsets

Given 1+((4n choose 2n) - (2n choose n)^2)/2 distinct, half-sized

subsets of a set with 4n elements, must there be two subsets which

intersect only in one element? (As problem P1, 250 pounds is offered.)

$500. (T1G) Uniformity of distance in the plane (I)

Is there a real number c such that n points in the plane always

determine at least cn/sqrt(log(n)) distinct distances?

$500. (T1G) Uniformity of distance in the plane (II)

Is there a real number c such that given n points in the plane, no more

than n^(1+c/log(log(n))) pairs can be unit distance apart?

$500. (P2) Sets with distinct subset sums

Is there a real number c such that, given a set of n positive integers

whose subsets all have distinct sums, the largest element is at least

c2^k? (As problem T1N, no prize is mentioned.)

$250. (P4) Collections of sets not represented by smaller sets

Is there a real number c such that for infinitely many positive

integers n, there exists cn or fewer sets with n element s, no two of

which are disjoint, and every n-1-element set is disjoint from at least

one of them?

$250/$100. (P15) Slowly increasing Turan numbers

If H is a (simple) graph, the Turan number T(n,H) is the largest number

of edges a graph with n vertices can have without containing a copy of

H. Conjecture: the function f(n) = T(n,H)/n^(3/2) is bounded above if

and only if every connected subgraph of H has a vertex of valence 1 or

2. The larger award would be granted for a proof.

$100/$25000. (T6N) Consecutive early primes

An early prime is one which is less than the arithmetic mean of the

prime before and the prime after. Conjecture: There are infinitely

many consecutive pairs of early primes. The larger award would be

granted for a disproof.

$100. (T8G) Quadrisecants in the plane

Given an infinite sequence of points in the plane, no five of which are

collinear, let r(n) be the number of lines that pass through four

points among the first n. Can it happen that r(n)/n^2 does not

converge to zero?

NOT A LETTER FROM KEN WOOD

. . . Though I can't imagine why you would, I ask anyway that you please not reprint this.

Cordially,

Ken Wood

[Editor's comment: I was very entertained by your letter, but you've asked me not to share it. So please send some stuff which I can print. This goes for everybody else as well.]

LETTER FROM DONALD SCOTT

Dear Rick,

Thanks for your response to those questions I asked you.

New questions

1. Would you recommend the study of logic, statistics, probability, and critical thinking since I'm so interested in learning to use my mind. Also, if you recommend any of the above could you provide me with names and authors so that I could purchase some books about each of the above subjects?

2. I would like to know if it is possible to obtain some issues of the Mega Society's old journal before they merged. Whom should I contact, and how much are back issues?

[Editor's reply: I definitely recommend statistics and probability. I'm too lazy for logic, and I don't know much about critical thinking as a field of study. My favorite statistics book is a thin yellow paperback called Error Analysis, by Taylor (I think). There's a picture of a wrecked train on the cover. It was my textbook for two different physics courses, one of which I even passed.

Jeff Ward was the pre-merger editor of the Mega Society journal. His address is 13155 Wimberley Square #284, San Diego CA 92128. However, unlike me, he has a life.]

VARIOUS YOUTHFULLY ENERGETIC CORRESPONDENCE FROM KEVIN SCHWARTZ

Dear Mr. Rosner:

Your name rings a bell from my grade school days; didn't you tie with Gov. Sununu in an Omni contest? I wish to subscribe to The Megarian; since I lack qualifying scores, for now I wish to subscribe as a non-member. Please send information. thank you for your time.

Sincerely yours,

Kevin Schwartz

Chairman, Greater Boston Chapter

The Thousand

P.S. Enclose: three juvenilia "sonnets". Perhaps you have the time and interest in corresponding?

{Editor's comments:

A. I'm a terrible letter writer. Correspondence fills me with dread. I file letters to which I must respond, find then weeks later, get scared, and hide them again. I like the telephone. Nevertheless, please send letters. The last few months have been filled with stuff that's lowered my already low efficiency--suicide, cancer, school, real estate agents. I've put all of this behind me and am ready to find new excuses.

B. Can never remember the definition of Noesis. Looking it up, I find that it means cognition.

C. We publish whatever, with a preference for brevity. For $20, Chris Cole can send you a complete set of back issues. As publisher, Chris likes to limit each issue to 20 pages. I'm willing to run your sonnets 'cause they're short, camera ready, and not too sappy. I skipped your short story.

D. Other Mega members/subscribers would probably be very pleased to correspond. There might be a few your age. There are two or three members/subscribers in Massachusetts.

E. Those wacky centa-Megarians: Hart used to submit stuff; he moved to some alternate virtual reality a couple years ago. Harding submits stuff. I especially liked his Multimax Test. The English-speaking world has a preponderance of super-high-IQ people because IQ testing is a ridiculous damn thing, just like western civilization. Sometimes Hard Copy runs out of "Cheerleaders Who Kill." They then do a segment on "Deranged Geniuses." The English-speaking world also has a preponderance of men and women with abnormally-large pectoral areas. Like high-IQ, this is also a media-induced phenom. As you might guess, the major diff between generic and centa-Megarians is that centa-Megarians show up more often in the tabloids. My theory is that a generic Megarian could ascend to centa status by getting a boob job or kidnapping Chelsea Clinton's cat.

F. I cope with philistine co-workers using a spectrum of techniques based on being meaner and crazier than they are. Stuff that works well for me--eating beer bottles, disrobing at parties & hitting other guests in face w/ my underpants, abusing customers. However, I'm getting too old for such misbehavior, so lately I just pay co-workers to be my friends.

G. Ten out of the fourteen people you ask about are past or present Mega members.

H. Any Mega members showing any sign of pre-Terman type genius will be asked to leave. (Seriously, there are so me very competent Mega members. Some even make the big bucks. Cole is optimistic that we could get together and change the universe, but so far we haven't. I think many members have points of view about the world that are way ahead of our time, but no one has convinced society yet.)

I. Hoeflin hasn't yet published the Ultra and Hyper Tests, but I'd guess that the Ultra will be published in '93.

J. No one I know of has found the three cube problem trivial or algebraic. It's considered the hardest problem on the Mega Test. I missed one verbal & two math & skipped one math.

K. I dunno what the FBI does.

L. A. Palmer, 609 W Washington St Apt 11-69, Sequim WA 98382