HIGH RANGE TESTS
Chris Cole
Chris Langan argues:
You [me] made the following two statements. "It is enough for me to know that the authors of the tests (taken by Paul Maxim) do not claim that they can be used to distinguish at the one-in-a-million level. I think we should believe them." In the interest of fairness, let me add the following equally valid statements. "It is enough for me to know that the authors of the tests (taken by Paul Maxim) do not claim that they cannot be used to distinguish at the one-in-a-million level. I think we should believe them." See? Now things are back in balance. Tests like the Pintner may be "low range" in comparison to tests like the Mega, but their ranges are more than adequate for a sufficiently young (mega-level) child.
In issue 126, 1 stated that I would not spend time discussing the concept of "range" in testing because I felt the members already understood it. From the above it is clear that at least one member does riot. First of all, let me explain why I do not think childhood IQ scores can be used for admission to Mega. A childhood IQ score is frequently computed using "mental age" divided by "physical age," so that a person scoring 200 at the age often has done as well on the test as an average person of twenty. However, we also hear that IQ as measured by several popular tests has a mean of 100 and a standard deviation of l6. How can these both be true? The answer is that near the mean (100) the population is roughly normally distributed, with a standard deviation of 16. Out near the Mega level, the distribution looks nothing like the tail of a bell curve, and we certainly cannot conclude that someone scoring 176 on a childhood IQ test is at the one-in-a-million level.
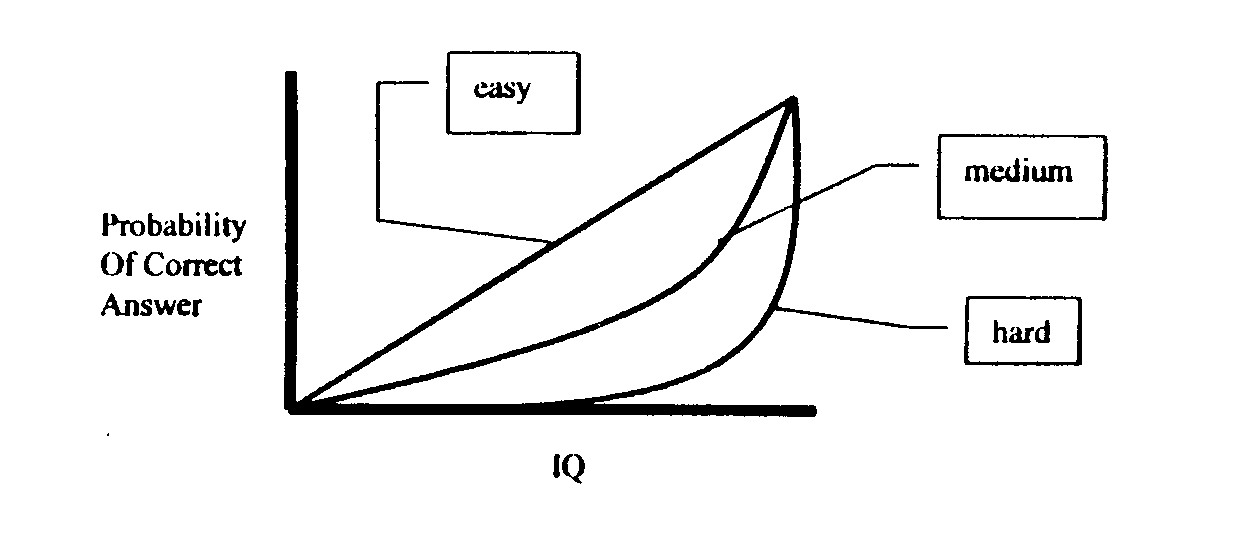
Secondly, the designers of IQ tests are trying to find out where people are near the meam; they are not trying to explore the Mega level. Cynics would point out that this is because there is no market up there. I'm sure that is part of the story, but in addition we should recognize that many of these tests are intended to diagnose learning disabilities, so that if they deviate from the mean at all, they conccnuatc on the low side. The purpose of the tests is to distinguish people who are near or below the mean. A test designed to do this must be composed of relatively easy problems. To see why, I have run a simulation. I created thrlv different "tests" - one easy, one medium, one hard. T'he easy test is composed of 500 easy problems, the malium test is composed of 500 medium problems, and the hard test is composed of 500 hard problems. What is an easy, medium or hard problem? A graph explains it better than words:
Graph of Problem Difficulty

The histograms below show the results of the simulated taking of this test by 10,000 "people." The people were uniformly distributed across intelligence, except two extra points were added at the high end. Intelligence is measured on an arbitrary scale from 0 to 1; a person with intelligence of 0.5 is five times more likely to correctly answer an easy problem than a person with intelligence of 0.1, for example. The asterisks on the histograms represent two standard deviations around the mean for each intelligence level. What the test designer is looking for is to make sure that the lines for 0.5, for example, do not overlap the lines for 0.4 or 0.6.
These histograms show that the easy test does a good job of spreading out the people with intelligence from 0.1 to 0.8, and a poor job above this. The hard test, on the other hand, does a poor job of distinguishing intelligence below 0.5, and better above this.
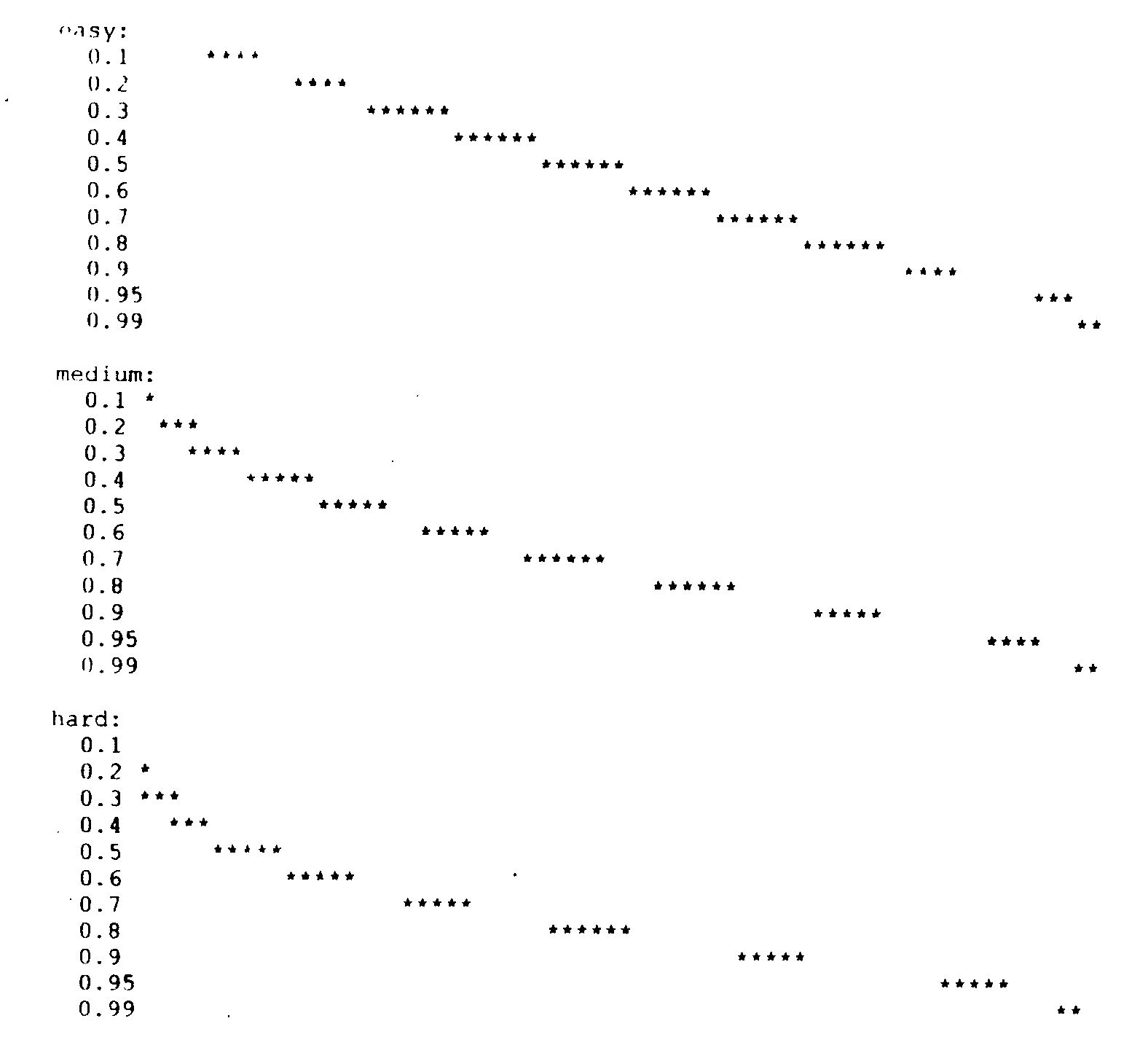
Thus, we do not need to be explicitly told by the designers of the
Pintner test, or any other standard intelligence test, that they are not valid in the Mega
range. If they were valid in the Mega range. then they would be useless in the normal
(100) range. It is simply impossible to design a test that is valid in both ranges. This
has nothing to do with the number of people that took the Pintner test, how big the
norming sample was, what the intended age of the tcstees was, etc. To claim otherwise is
bad science.