Brian Schwartz' Application for Mega Membership
Kevin Langdon
In Noesis #163, Ron Hoeflin printed a letter from Brian Schwartz containing his application for membership in the Mega Society, based on his SAT score. Unfortunately, there are some questionable assumptions involved in the arguments that have been made for the adequacy of this test, even with near-ceiling scores, as an admission instrument for the Mega Society.
Mr. Schwartz' letter previously appeared on the mega e-mail list at Yahoo!Groups (any Mega member who wishes to join this [low-traffic] list should e-mail me and I'll add him or her to the distribution) and was discussed there. I have compiled the relevant messages from that list for publication in Noesis. See "E-mail on the Mega List at Yahoo!Groups Regarding Brian Schwartz' Application for Admission to the Mega Society," in this issue. These messages are reproduced here because Mega members need to be able to cast fully-informed votes on the proposal by Dr. Hoeflin to admit Mr. Schwartz to the society.
Here is Mr. Schwartz' letter, with my comments:
Dear Sirs:
I believe that my test scores make me eligible for consideration for membership in your society.
In 1967, at the age of fourteen, I took the S.A.T. My score was 1593--793 in English and 800 in Math. According to Ron Hoeflin's Fifth Norming of the Mega Test, see also the Prometheus Society's 1998/99 Membership Committtee Report, section 8.5.6, in an average year only six people achieved a score of 1590 or higher.
This is precisely why the meaning of extremely high scores cannot be reliably be determined by the distribution of scores at the high end. Six people make up too small a sample to be statistically meaningful. And a scarcity of near-ceiling scores is often due to "ceiling bumping," composed of errors in the test itself and careless errors on the part of the testee, which artificially limits the performance of the highly capable. The significance of very high scores must be extrapolated from the distribution as a whole.
For a discussion of ceiling bumping see my letter in Noesis #140 at:
http://www.polymath-systems.com/intel/hiqsocs/megasoc/noes140/langdon.html
As ceiling bumping artificially reduces scores very close to a test's ceiling, we can add about one IQ point to these scores to compensate, as should be clear from the untitled figure included in the letter cited above. An SAT V+M score is approximately an IQ score times 10; this would put Brian's score at 1603, 3 raw score points above the SAT ceiling.
Mensa has spent considerable effort establishing that the 98th percentile on the old (pre-1995) SAT is 1250 (V+M). The 99.9th-percentile societies have come to the conclusion that the 99.9th percentile is variously 1450, 1460, or 1470. My best estimate is 1460. Table 1 below, which is based on the ETS tables of SAT scores printed in Noesis #165, shows the tested-group percentiles corresponding to 1250 and 1460, for the years 1984-1988, for the United States.
Table 1. SAT Percentiles Corresponding
to the 98th and 99.9th percentiles, 1984-1988
98 99.9
Year (1250) (1460)
1984 95.0 99.8
1985 93.8 99.7
1986 93.6 99.7
1987 93.4 99.65
1988 93.8 99.7
The median figure for the 98th percentile is 93.8 and for the 99.9th percentile is 99.7. As approximately one million students took the test each year, out of a total age cohort of three million, and it is likely that almost all those at the 98th percentile or above take the SAT, the percentiles above must be adjusted by about a factor of three to obtain general-population percentiles. This comes out to the 97.9th percentile for 1250, just slightly below the 98th percentile, and the 99.9th percentile for 1460, right on the money.
With the societies' cutoff scores thus verified, we may now project them to discover where higher levels occur. This raises the question of the appropriate method for projecting them. The simplest and most common method for establishing the relationship between scores on different scales is to equate the means and standard deviations for the distributions.
Mensa's cutoff is about 2.05 standard deviations above the mean and the cutoff for TNS and the other 99.9th-percentile societies is about 3.1 SD's above the mean; therefore 4.15 SD's above the mean should be reached at approximately 1670. (Using straight-line methods further down the scale is problematical because the assumption that essentially all testees at a given level take the SAT breaks down.)
Table 2. Standard Deviations Above the Mean and
Percentiles
Corresponding to Scores on the Pre-1995 SAT
SD's Above the Mean Percentile Old SAT (Verbal+Math)
4.75 99.9999 1795
4.15 99.9985 1670
4.00 99.997 1655
3.70 99.99 1600
3.10 99.9 1460
2.05 98 1250
Brian Schwartz continued:
And, according to Ron Hoeflin's Sixth Norming, see also the Prometheus report, section 8.5.4, virtually all high school seniors in the 99th IQ percentile or higher took the SA.T. Since there were three million seniors (aged 17) in 1967, a seventeen-year-old with a score of 1593 would have scored in the 99.9998th percentile.
This disregards the considerations I outlined above and Chris Cole's argument using the example of the distribution of coin-flipping trials in "The Discrimination Power of the SAT," published in Noesis #164. The very small numbers of extremely high scores indicate at least some ceiling-bumping. Very few people have scored above the ceiling, but that doesn't prove anything either. ;-)
But since I was 14, and a junior, my percentile rank would be higher. A 14 year old who does as well as a normal, average 17 year old has a ratio IQ of slightly over 120.At that level ratio IQs are more or less equivalent to deviation IQs. See http://www.geocities.com/ultrahiiq/Deviation_IQs.html.
There are some errors at the highest levels listed in this table, but they make no difference to the current discussion. However, it is not true that deviation IQ's are equivalent to ratio IQ's for teenagers.
And a deviation IQ of 120 is about the 90th percentile (for both 15 and 16 SD) See http://members.shaw.ca/delajara/IQtable.html
This would put my score far above the 99.9999 level, eligible for Mega.
The tables are standard but Brian is leaving important considerations out. As has been demonstrated above, 1600 on the old SAT corresponds to about 3.7 standard deviations above the mean, IQ 160. The ratio method of age adjustment would yield an IQ of about 194, but the relationship between mental age and chronological age departs markedly from linearity by the ages in question.
An excellent presentation of the model of the increase of cognitive ability with age underlying ratio IQ appears on pages 24-27 of The Measurement and Appraisal of Adult Intelligence, by David Wechsler (4th Edition). These four pages are reproduced in this issue of Noesis. An approximate representation of the relationship between mental age and chronological age described in this chapter is contained in Figure 1. (A similar figure appears as Figure 4.25 on page 104 of Jensen's Bias in Mental Testing.)
Figure 1 quantifies the leveling off of raw intellectual power as a function of age, according to a relatively optimistic model that allows for a significant amount of gowth of cognitive power during the late teens. Even under this model the departure from a straight ratio calculation is apparent.
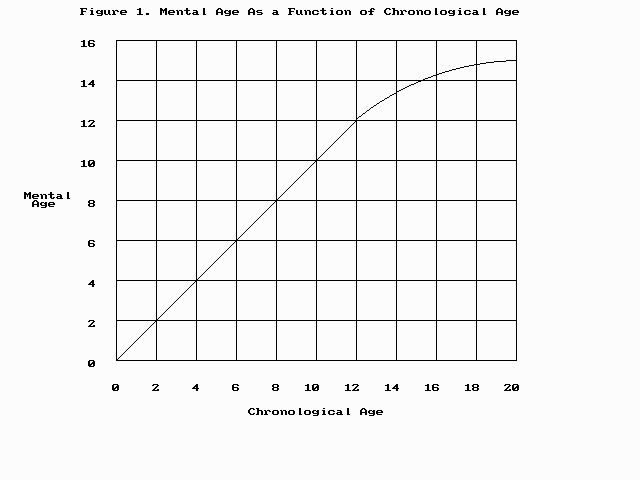
There's a straight-line relationship between chronological and mental age for young children but this relationship breaks down after about age 12; mental age increases to a maximum of about 15 by the chronological age of about 20, remaining almost steady thereafter but declining slowly into late middle age, after which it declines more rapidly.
The mental age (as defined in this context) of a 14-year-old is approximately 13.3 and of a 17-year-old is 14.8. Thus Brian's 1603 must be multiplied by 14.8/13.3 = 1.11, not 17/14 = 1.21, to obtain 1784, or about IQ 175, one point below Mega's cutoff. But this is a ratio adjustment. Ratio IQ tests are known to yield many too many very high scores. Robert Dick has suggested that ratio IQ may be distributed log-normally. An article by John Scoville, "Statistical Distribution of Childhood IQ Scores," develops this idea and shows that it corresponds very closely to the actually-observed incidence of ratio IQ scores:
http://sweb.uky.edu/~jcscov0/ratioiq.htm
A ratio IQ score of 175 would be equivalent, according to the table in this article, to a deviation IQ of only 160, 3.75 sigma, a full standard deviation below Mega's cutoff level. Interpolating in the table on page 11 of Noesis #163 [in "Comparing `Normal Curve' (Galton) vs. `Original Stanford Binet' (Terman) Scales of Intelligence," by Ronald K. Hoeflin] gives a similar, but slightly more pessimistic, result. Dr. Hoeflin estimated, in that essay, that 1575 is the 15-per-million level, meaning that 1600, approximately 2.5 IQ points higher, would be at about the 8-per-million level, still a bit short of the Mega level.
A ratio-IQ/deviation-IQ conversion table, which works very well in explaining the observed frequency of high scores on the Stanford-Binet and similar instruments, is obviously not precisely applicable to SAT scores; the ratio-to-deviation-IQ adjustment would nullify the entire age adjustment, which is absurd. But the IQ age adjustments certainly put into question the assumption that an appropriate SAT age adjustment can be obtained simply by calculating a ratio.
In addition to its limited ceiling, the SAT has a problem with discrimination at the level of interest because the level of difficulty of its items is too low, as Chris Cole has pointed out. And another relevant question is whether high scores just a little earlier than the nominal age at which performance plateaus are the result of precocity rather than real intellectual superiority.
But is the SAT an acceptable test for admission purposes? I believe it is.
I disagree. The present essay outlines my reasoning.
The SAT has been given every year since 1926. Over a million people take the test every year. It is possibly the most carefully studied, normed, and scrutinized test in history.
The SAT correlates highly with g. (See A. Jensen, *The g-factor*, N. Lemann, "The Great Soritng" (Atlantic Monthly, Sep. 95), Prometheus Society Membership Committee Report, section 8.5)
These are true and significant facts. The SAT is a good test. The problem is with its ceiling and the meaning of high scores.
The hundreds of questions on the SAT all test mental abilty (fluid g) and do not rely on learned knowledge (crystallized g)
That's too strong a statement. There's some loading on general and academic knowledge, but the SAT is primarily a measure of g.
Because of this high g-loading, Ron Hoeflin relied on SAT scores to norm his Mega test. Indeed, he believed that the SAT was valid at the 99.9999 level, but could not use it because he didn't have enough data: "I had hoped that with data on over 5 million SAT test subjects I would be enabled to refine my norms for the upper end of the Mega Test scale, in particular permitting me to pinpoint the one-in-a-million level more accurately. Unfortunately, this goal could not be achieved by means of this extra data since the number of SAT scores reported to me by Mega Test participants, 222, remains inadequate." (Sixth Norming)
I don't see how Brian drew the conclusion that Dr. Hoeflin "believed that the SAT was valid at the 99.9999 level" from the quoted passage.
I hope the above helps you with my application. I am honored to be considered for membership in your society.
Brian Schwartz
Treasurer, Prometheus Society
Ron Hoeflin appended:
Editor's Note: In my opinion Brian Schwartz's SAT scores qualify him for membership in the Mega Society based on the one-in-a-million admission standard, given his age at the time he took the test. Since we do not currently accept the SAT as an admission test due to a mutual agrement [sic] between Chris Cole and Kevin Langdon, who have held the strings of power in this Society, at least until recently, we need to have a vote by the members to overrule them and admit Mr. Schwartz as a member. Any comments on this issue for publication in Noesis should be submitted promptly.
Ronald K. Hoeflin
Mega admission scores are not set by "mutual agreement between Chris Cole and Kevin Langdon"; they're set by vote of the membership. The latest membership vote on this question accepted the Titan Test as our sole qualifying instrument. I opposed this, on the grounds that it has been reported that answers to the Titan Test have appeared on the Internet, but the motion passed and I deferred to the wishes of the membership. This canard against Chris Cole and me is totally unjustified.
This essay and the supporting materials I've assembled represent my response to Ron's argument for acceptance of Brian Schwartz as a member of Mega based on his SAT score. As Chris Cole and I have argued, it is not a good idea to accept Mr. Schwartz as a member at this time, for the following reasons:
1. The SAT is not designed to discriminate at, or anywhere near, the one-in-a-million level.
2. The Mega Test norms on which the one-in-a-million claim is based are inflated at the high end.
3. Age-correction of scores is a highly dubious proposition and a high score "for one's age" does not necessarily indicate truly superior adult reasoning ability.
4. We should set our qualifying scores first and accept applications based on them afterwards. And when we agree to accept a test for admission purposes we should determine what our qualifying score on the test will be. Evaluating applications based on tests not on our list of qualifying instruments as they are received invites subjective decision-making and weakens our admission standards.
5. The Titan Test is available as an alternative.
Please vote "no" on Dr. Hoeflin's proposal.