A logic and semantics for imperatives
Ian Williams Goddard
| Truth is undefined for imperative statements. However, if imperatives implicitly reference a fact, they can be rephrased as truth-valuable declaratives explicitly referencing that fact. But are there such facts? Kenny held that any imperative references a set of wishes held by its imperator. I extend his thesis by proposing that imperator wishes are facts implicitly referenced by imperatives and explicitly referencing them yields semantically isomorphic declaratives. I implement this thesis with modal operators for wants and cause with which declarative schemata are formed to automate translation of imperatives into semantically isomorphic declaratives called proxy-imperatives. The proxy-imperatives match imperative behavior and provide semantic validation of imperative arguments thereby integrating imperative reasoning into classic truth-valuable logic. |
1. Introduction
1.1 The problem
Formal semantics defines criteria for evaluating the truth of declarative statements with respect to domains of discourse. However, imperative statements like “Shut the door!” are not obviously true or false in any domain and therefore fall outside the realm of truth-valuable statements. Without truth values imperative arguments cannot be shown to be truth preserving, or semantically valid, even if they are intuitively valid. As such, it is held that imperative arguments, which form a large body of everyday arguments, fall outside the scope of formal logical reasoning. This paper proposes to bring them in scope.
1.2 The path followed
Given their lack of truth values, proposed imperative logics often define alternatives to truth. An important example is Anthony Kenny's substitution of being satisfactory in place of being true. An imperative is satisfactory just in case obeying it will satisfy the wishes an imperator intends to express. So for example, if I want someone to close the door, the statement “Shut the door!” is satisfactory because its fulfillment by a listener will make my wish come true. Given this alternative to truth, Kenny proposed that just as the goal of classical declarative logic is to preserve truth, the goal of an imperative logic should be to preserve wishes from assumptions to conclusions in imperative argumentation.(1)
Kenny's wish-preserving criterion is intuitive. For example, from “Shut the door!” one should not expect it to be possible to infer any imperative that upon obeying keeps the door open. This gives us important insight into both what we want an imperative logic to do and what imperatives are. Even Kenny's critics didn't dispute his wish-preserving criterion but faulted his logic instead for its failure to actually preserve wishes.(2)(3) But for us here, what matters is Kenny's insight that an imperative denotes a set of wishes -- an insight we'll implement explicitly. We'll avoid the problems raised against his logic by relying on classic truth values acquired by translating imperatives into truth-valuable declaratives that directly reference the contents of an imperator's set of wishes.
Translating imperatives into declaratives to express their meaning is not new. For example, H. G. Bohnert proposed: “There exists a set of grammatically declarative sentences which can be put in one-to-one correspondence with commands.” He posited such a mapping wherein any command A can be translated into a declarative of the form Either obey A or else M will happen, where M is a motivating factor intended to compel compliance.(4) R. M. Hare also explored this approach, noting that for any declarative describing an event, “we can frame a corresponding imperative sentence commanding that event to happen.” (5)(6) In contrast, I simply propose that declaratives denoting what an imperator wants are the most suitable declarative translations for imperatives.
2 The wants premise
Kenny's premise that an imperative expresses an imperator's wish for a goal state is my premise too. By this premise, what an imperator means is what the imperator (or anyone compelling them to speak) wants. This is the natural interpretation of imperatives. If you are told “Do it!” you assume someone wants you to ‘do it', otherwise the statement is not a true command. So we shall define declaratives that express the meaning of imperatives such that the declaratives are true just in case an imperator actually wants done what his or her imperative instructs listeners to do. Such imperatives are said to be sincere.
It should be noted that Hare has observed that imperatives can be translated into declaratives denoting what an imperator wants such that saying “Shut the door” means the same as “I want you to shut the door.” (7) But he built no analysis from that. Figure 1 below illustrates the concept underlying my thesis that shall be rigorously implemented.
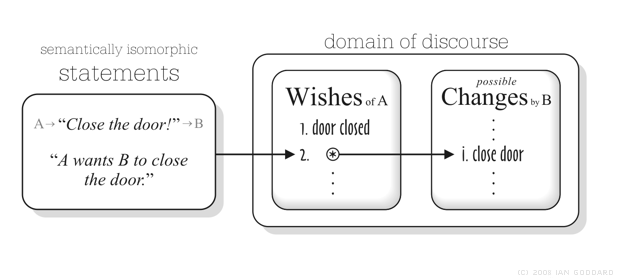
Figure 1. Thesis: for any imperative there's a semantically isomorphic declarative that explicitly references an imperator's wish for a listener-caused change (2) that makes a primary wish (1) true.
To flash forward briefly, the semantic structure in Figure 1 shall be explicitly implemented with modal operators that denote Wishes and possible Changes above. Given a set of conceivable states of affairs S = {r, s, t, … }, Wishes maps members of a set of agents A = {a1, … , an} to members of the power set of the cross-product of S, P(S´S), whose members are sets of state pairs. So for example, suppose for simplicity that Wishes(a1) = {(s, u)}, then the set of wishes of agent a1 contains one wish (s, u) that means: in state s agent a1 wants state u. Changes shares the same structure except that if Changes(a1) = {(s, u)}, then (s, u) means: in state s agent a1 can cause state u. This semantic structure is illustrated below in Figure 2 showing a subset tree of P(S´S).
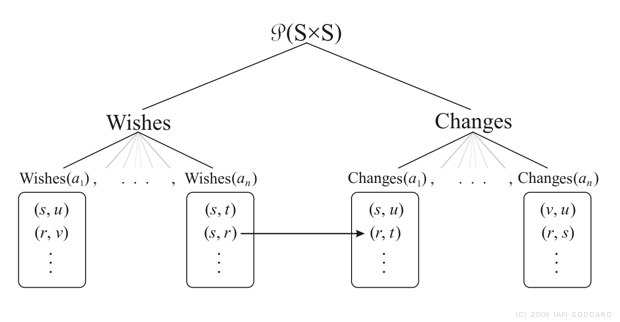
Figure 2. A subset tree of P(S´S) forms a modal frame used to formally implement the conceptual semantics seen in Figure 1. Wishes and Changes form subsets of P(S´S) that contain sets of state pairs where each set represents an agent's wants or state-transitions they can cause. The arrow in Figure 2 replicates the arrow in Figure 1 (except agents A and B there are here an and a1 respectively). The arrow also represents the mapping of the proxy imperatives we'll define with Wishes and Changes.
The objection might be raised that wanting is a mental state, and mental states are not properly objects of formal logic. However, epistemic modal logic defines operators for knowledge, and knowing is also a mental state. So it's not the case that mental states can't be objects of formal logic. Now, let's define a language to implement the wants thesis.
( If logic symbols don't view properly with your browser, see the PDF version. )
2.1 A proxy-imperative language L
The language L defines agent-specific modal operators for wants and cause. L is similar in construction to epistemic logics. For example, Fagin et al.(8) define knowledge operators indexed to intelligent agents such that for n agents there are K1, … , Kn operators where each Ki means “Agent i knows” and so Kiφ means “Agent i knows φ ” where φ is a proposition variable. We'll also define modal wants and cause operators that are specific to agents. Let us then begin with a generative grammar for L.
DEFINITION 1 (language L). Given a vocabulary = á P, N, U, B, M, A ñ composed of six sets of atomic propositions P = { p, p', p'', …}, names N = { n1, … , nn }, unary connectives U = { Ø }, binary connectives B = { ® , Ù , Ú }, modalities M = { [ω], áωñ, [c], ácñ }, and auxiliary symbols { (, ) } the formulae of L form the smallest set F such that:
1. If p Î P, then p Î F.
2. If φ Î F, then Øφ Î F.
3. If * Î B, and φ, ψ Î F, then (φ * ψ) Î F.
4. If [•], á•ñ Î M, n Î N, and φ Î F, then [•]n (φ) , á•ñn (φ) Î F.
The syntactic structure for the proxy-imperatives we'll define appears in 1.4 above. The ω modality means wants and the cmodality means cause, which in Greek would be the leipeic and aitic modalities respectively. Each type • has two modes, one mode [•] expresses necessity and the other á•ñ possibility. Accordingly, these modes shall have these preferred English interpretations (where φ is an arbitrary formula in F):
1. [ω]n (φ) reads: n must have φ.
2. áωñn (φ) reads: n accepts φ.
3. [c]n (φ) reads: n must cause φ.
4. ácñn (φ) reads: n can cause φ.
Other translations are possible. Instead of 'must have' in mode 1 above we could say 'requires'. As for mode 2 above, 'accepts' may in some cases be replaced with 'likes', and so 'loves' might replace 'must have' in mode 1 since likes and loves reflect weaker and stronger modes of wanting. A number of English terms point in similar directions and could be chosen to describe specific situations in various domains of discourse.
Both wants and cause modalities have classic modal negation transformations with intuitive translations (left as an exercise for curious readers).
[•]n (φ) Û Øá•ñn (Øφ) |
á•ñn (φ) Û Ø[•]n (Øφ) |
[•]n (Øφ) Û Øá•ñn (φ) |
á•ñn (Øφ) Û Ø[•]n (φ) |
So for example, á•ñn (Øφ) is the negation-normal form of Ø[•]n (φ), and each can replace the other due to their equivalence. Now we introduce the proxy-imperative schemata.
2.2 Proxy-imperative schemata
From the modes of wants and cause the proxy-imperative schemata are formed:
1. [ω]n [c]n' (φ) reads: n must have it that n' must cause φ.
2. [ω]n ácñn' (φ) reads: n must have it that n' can cause φ.
3. áωñn [c]n' (φ) reads: n accepts that n' must cause φ.
4. áωñn ácñn' (φ) reads: n accepts that n' can cause φ.
These are the statement schemata we'll use for proxy-imperatives. It's essential to note that they do not denote imperative statements but rather facts that hold true about any imperator. The proxy-imperatives denote preconditions for the utterance of imperatives that also hold true concurrently with imperative utterance. Proxy-imperatives can be true even if no imperative is uttered. To denote in our translations that the utterance of an imperative has occurred, 'must have it' in 1 above may be replaced with 'demands' or 'commands'. And 'asks' or 'requests' may replace 'accepts' in 3 and 4. Not expressly denoting an utterance, 'allows' or 'permits' may also replace 'accepts'. Many English terms point in similar directions.
Schema 1 denotes conditions underlying the strongest imperatives, commands, which denote the highest degree of wanting and of necessity of compliance. On the opposite end, schema 4 models requests, the least urgent and most polite imperatives like: “If possible, please pick up some milk after work,” or “Could you please pass the salt?” The four proxy-imperative schemata can cover a wide range of imperative statements.
L AXIOMS: for all [•], á•ñ Î M, all n, n' Î N, and any φ Î F we accept as true:
1. [•]n (φ) Þ á•ñn (φ)
2. [ω]n [c]n' (φ) Þ áωñn (φ)
In the case of wants (ω), Axiom 1 says: if n must have φ then n accepts φ. Obviously, if I must win, I'll accept winning. For cause, Axiom 1 says: if n must cause φ then n may cause φ. These are both not only intuitive but Axiom 1 also prevents vacuous truth for the necessary modes in our semantics, as we shall see shortly. Axiom 2 says: if n must have it that n' must cause φ then n accepts φ. Axiom 2 says all imperatives are sincere.
2.3 Proxy-imperative behavior
Now we'll compare proxy-imperatives with real imperatives. First, observe that because the minimal mode of wanting áωñ denotes what is acceptable, a negated proxy-imperative command is not a model for a contrary command but instead for contrary permission.
Ø[ω]n [c]n' (φ) = áωñn ácñn' (Øφ)
It's not the case that n demands n' must cause φ = n accepts that n' may cause not-φ
That equivalence implies that the negation of “Shut the door!” is not the contrary command “Don't shut the door!” but the contrary permit: “You may leave the door open.” So according to the proxy-imperatives of L, a negated command repeals the command and permits contrary behavior. This in fact matches natural commands of which public laws are canonical. Take for example the military draft. What happens when we repeal a command by a leader that any man, let's say Jon, must enlist? Let's see (the proposition p that's commanded to be made true is 'Jon is enlisted.')
(a) [ω]leader [c] jon ( 'Jon is enlisted.' )
Reads: The leader commands that Jon must enlist.
So the negation of command a above is by negation normalization b, c, and d:
(b) Ø[ω]leader [c] jon ( 'Jon is enlisted.' )
Reads: It's not the case that the leader commands that Jon must enlist.
(c) áωñleader Ø[c] jon ( 'Jon is enlisted.' )
Reads: The leader accepts that Jon need not enlist.
(d) áωñleader ácñ jon ( 'Jon is not enlisted.' )
Reads: The leader accepts that Jon may not enlist.
So according to both our proxy-imperatives and natural intuition, repealing a draft's command “Enlist!” does not mean “Don't enlist!” but rather: “You may not enlist.” (This intuitive result suggests that there's an inherent modal structure in imperatives.) Obviously no person who understands the repeal of a draft would fear arrest for enlisting as they would not interpret its negation as a command against enlisting. The example above shows that natural language and intuition behave like the proxy-imperatives such that in both systems a negated command is not a contrary command but contrary permission.
2.4 A proxy-imperative semantics
And now let's explore the meaning, or semantics, of L and its proxy-imperatives. We do that with a model for L that defines a frame of objects and relations between them from which domains of discourse can be built and in which, by way of an interpretation, the statements of L have their meaning. Here then is such a model for L.
DEFINITION 2 (model ). A model for language L is M = á S, A, Wishes, Changes, α , V ñ where
á S, A, Wishes, Changes ñ is a domain frame and á α, V ñ is an interpretation for L:
1. S is a non-empty set of conceivable states of affairs: S = {s, s' , s'' , … }.
2. A is a non-empty set of intelligent agents: A = {a1, … , an}.
3. Wishes : A ® P(S´S) assigns to each agent a set of wishes in P(S´S) containing state pairs such that if (s, s' ) Î Wishes(a), then in state s agent a wants state s' .
4. Changes : A ® P(S´S) assigns to each agent a set of causable state transitions in P(S´S) such that if (s, s' ) Î Changes(a), then in state s agent a can cause s' .
5. α : N ® A assigns names to agents such that α(n) is the agent named n.
6. V : P ® P(S) is a valuation function that assigns to each L proposition a set of states such that if V(p) = { s, s' }, then proposition p holds true in states s and s' .
The L frame requires a wider set of states to draw from than an alethic frame because wanting casts a wider net over states than alethic possibility given that one can want the impossible. For example, you could want to be as big as a mountain or to travel in time, but such conceivable states are not possible states. So in the L frame the set of states S contains conceivable states that may be impossible but sill wantable. On the other hand, Changes does assign access relations to agents. For all a Î A and all s, s' Î S, if (s, s' ) Î Changes(a), then state s' is possible from state s, and perhaps because agent a can cause s' . Conceivable states are plausibly infinite and possible states are a proper subset of S.
2.5 defines a name-assignment function α such that for any name n Î N, α(n) is the intelligent agent named n in the domain of discourse.(9) If for any agent a Î A we have it that a = α(n), then Wishes(a) = Wishes(α(n)). So we may represent the arbitrary agent by either a or α(n), and we use α(n) in Definition 3 below. Definitions 2.3 and 2.4 above are foundational to my imperative thesis and follow standard modal definitional structure with the exception that they serve to model modes of wanting and causability respectively rather than alethic possibility, deontic obligation, or epistemic knowing.
DEFINITION 3 (semantics). Given L model M, the truth conditions in any state s Î S are (where (s) ![]() φ is read: in state s, φ is true):
φ is read: in state s, φ is true):
1. (s)
p iff s Î V(p) .
2. (s)
Øφ iff (s)
φ.
3. (s)
φ ® ψ iff (s)
φ or (s)
ψ.
4. (s)
φ Ù ψ iff (s)
φ and (s)
ψ.
5. (s)
φ Ú ψ iff (s)
φ or (s)
ψ.
6. (s)
[ω]n (φ) iff for all s' Î S, if (s, s' ) Î Wishes(α(n)), then (s' )
φ.
7. (s)
áωñn (φ) iff for a s' Î S, (s, s' ) Î Wishes(α(n)) and (s' )
φ.
8. (s)
[c]n (φ) iff for all s' Î S, if (s, s' ) Î Changes(α(n)), then (s' )
φ.
9. (s)
ácñn (φ) iff for a s' Î S, (s, s' ) Î Changes(α(n)) and (s' )
φ.
By Axiom 1, in any L-model M, if (s) ![]() [ω]n (φ), then (s)
[ω]n (φ), then (s) ![]() áωñn (φ). So by Definitions 3.6 and 3.7, every agent wants at least one conceivable state. Otherwise, [ω]n (φ) can be vacuously true by Definition 3.6 when agent α(n) wants no state. This serial condition also blocks vacuous truth in alethic modal logic and applies to the cause modality such that every agent can cause at lest one state. Axiom 1 is intuitively valid as well.(10) Definitions 3.6 through 3.9 are unique and implement my thesis.
áωñn (φ). So by Definitions 3.6 and 3.7, every agent wants at least one conceivable state. Otherwise, [ω]n (φ) can be vacuously true by Definition 3.6 when agent α(n) wants no state. This serial condition also blocks vacuous truth in alethic modal logic and applies to the cause modality such that every agent can cause at lest one state. Axiom 1 is intuitively valid as well.(10) Definitions 3.6 through 3.9 are unique and implement my thesis.
Definitions for the proxy-imperatives follow directly from Definitions 3.6 through 3.9. However, it's worth presenting them explicitly. They are for brevity presented in meta-logic rather than the meta-language of English used for Definitions 3.6 - 3.9.
DEFINITION 3 (amendment - proxy-imperative definitions)
10. (s)
[ω]n [c]n' (φ) iff:
"s' "s'' [ ( (s, s' ) Î Wishes(α(n)) Ù (s', s'' ) Î Changes(α(n' )) ) Þ (s'' )
φ ]
11. (s)
[ω]n ácñn'(φ) iff:
"s' [ (s, s' ) Î Wishes(α(n)) Þ $s'' ( (s', s'' ) Î Changes(α(n' )) Ù (s'' )
φ ) ]
12. (s)
áωñn [c]n' (φ) iff:
$s' [ (s, s' ) Î Wishes(α(n)) Ù "s'' ( (s', s'' ) Î Changes(α(n' )) Þ (s'' )
φ ) ]
13. (s)
áωñn ácñn' (φ) iff:
$s' $s'' [ (s, s' ) Î Wishes(α(n)) Ù (s', s'' ) Î Changes(α(n' )) Ù (s'' )
φ ) ]
Figure 3 below extends Figure 2 by articulating the mapping on P(S´S) that builds the proxy-imperatives. Each proxy-imperative for some imperator agent α(n) explicitly denotes the set Wishes(α(n)) which is that agent's set of wishes. This is an explicit implementation of Kenny's thesis that an imperative denotes its imperator's set of wishes, but we extend from his thesis by adding the cause modes that conjoin with the wants modes to form the proxy-imperatives as part of what is wanted is a change or null-change.
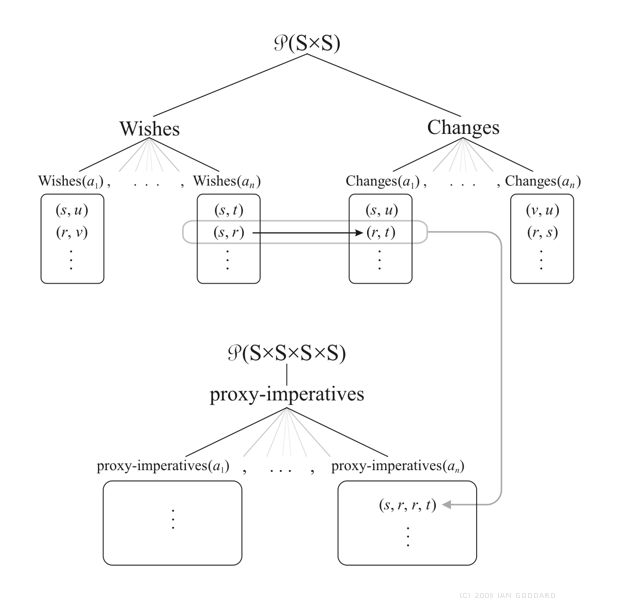
Figure 3 the subset tree of P(S´S) branches into subsets Wishes and Changes, each divided into subsets, one for each agent α (n). Implementing the concept shown previously in Figure 1, here we have an example of agent α (nn) in state s wanting agent α(n1) in state r to cause state t. The resulting mapping to and from P(S´S) forms a subset of P((S´S) ´ (S´S)) called proxy-imperatives which is divided above into subsets each of which contains state-quintuples that are preconditions for specific imperatives an agent may utter.
3 By proxy semantic validation of imperative argument
Now we put our proxy-imperatives to work to provide semantic proofs by proxy for imperative arguments. We assume that any meaningful imperative has an imperator and thus that there is at least one agent who wants it obeyed and whose name is i. Below, a natural-language imperative argument appears on the left (steps 1a, 2a, and 3a) and its translation into L appears on the right (steps 1b, 2b, and 3b). Assume for this argument that proposition p = 'You see Jesse' and q = 'The police are notified '.
| 1a. If you see Jesse, call the police! | 1b. p ® [ω]i [c]n (q) |
| 2a. You see Jesse. | 2b. p |
| 3a. Call the police! | 3b. [ω]i [c]n (q) |
PROOF: By 1b we assume that in model M, (s) ![]() p ® [ω]i [c]n (q). By Definitions 3.1 and 3.10 this means that we accept as true that if state s Î V(p), then for all s' , s'' Î S, if (s, s' ) Î Wishes(α(i)) and (s', s'' ) Î Changes(α(n)), then (s'' )
p ® [ω]i [c]n (q). By Definitions 3.1 and 3.10 this means that we accept as true that if state s Î V(p), then for all s' , s'' Î S, if (s, s' ) Î Wishes(α(i)) and (s', s'' ) Î Changes(α(n)), then (s'' ) ![]() q. Now, by 2b we have it as a fact that state s Î V(p); therefore, by assumption 1b and Definition 3.10 we also have it as a fact that for all conceivable states s' and s'' , if agent α(i) wants state s' and in state s' agent α(n) must cause state s'', then in state s'' proposition q is true, which is to say by Definition 3.10 again that we have it that: (s)
q. Now, by 2b we have it as a fact that state s Î V(p); therefore, by assumption 1b and Definition 3.10 we also have it as a fact that for all conceivable states s' and s'' , if agent α(i) wants state s' and in state s' agent α(n) must cause state s'', then in state s'' proposition q is true, which is to say by Definition 3.10 again that we have it that: (s) ![]() [ω]i [c]n (q). £
[ω]i [c]n (q). £
Since perhaps most imperative arguments can be expressed in modus-ponens form as above, and because the proxy-imperatives are declaratives, it's trivial that we can provide semantic validation for any number of proxy-imperative translations of imperative arguments in the way shown above. So there's no need to belabor the point that here we have a mechanism of providing by proxy semantic validation of imperative arguments.
4 Conclusion
The goal of this project has been to understand the semantic structure of natural imperatives and from such insight build a formal model of imperative semantics that can integrate imperatives into classical logic. So matching the behavior of natural imperatives has been both a goal and guide. Following the frequented path of defining alternatives to truth values in a new kind of logical system used only for imperatives was not an attractive option. My goal has been to facilitate semantic evaluation of imperatives within the same semantic machinery used to evaluate declaratives. Such a model of imperatives would be the simplest model as it only requires preexisting modal-logic infrastructure. I believe and hope that the proxy-imperatives defined herein, which are declaratives that I posit as semantically isomorphic to imperatives, may be either a sufficient model of imperatives that brings them into the scope of classical logic or at least a useful start on that path.
(1) Kenny, A. J. (1966). Practical Inference. Analysis, 26: 65-75.
(2) Geach, P. T. (1966). Dr. Kenny on Practical Inference. Analysis, 26: 76-79.
(3) Gombay, A. (1967). What is imperative inference? Analysis, 27: 145-152.
(4) Bohnert, H. G. (1945). The Semiotic Status of Commands. Philosophy of Science, 12(4): 302-15.
(5) Hare, R. M. (1949). Imperative Sentences. Mind, New Series, 58(299): 21-39.
(6) Most research on imperative logic was done between the 1930s and 1970s. For a short review of some recent work let me suggest: B. Žarnić's Imperative Negation and Dynamic Semantics: http://www.vusst.hr/~berislav/personal/MeanDynTurn.pdf
(7) Hare, R. M. (1952). The Language of Morals. Oxford, Oxford University Press, p 5.
(8) Fagin, R., Halpern, J.Y., Moses, Y., & Moshe Y. Vardi. Reasoning about knowledge. Cambridge, Massachusetts, MIT Press, 1995.
(9) Definition 2.5 might seem to add excessive semantic machinery, however, it better segregates L syntax and semantics. For example, in Fagin et al the number of modal operators K1, … , Kn in the language reflects the number of agents n in the domain.(4) But the number of modal operators in L syntax is independent of the number of agents in the domain. This abstracts the L modalities from domains. In natural thought, wanting and causing, as well as knowing, are concepts we've abstracted from our domains of experience such that we can conceive of them independent of specific instances. And so in natural language, wants, cause, and knows are atomic operators rather than Adam wants, Amy wants, … and so on, per person. For these and other reasons, I feel that the extra semantic machinery better models natural semantics.
(10) If you must have p, then you'll certainly accept p. So too, if you must cause p, you can cause p. The intuitive nature of Axiom 1 holds even in the extreme cases: (a) Even the most aesthetic Buddhist monk probably, for example, wants at least one thing, such as to not want anything else. And true non-wanting is classically (where it is held as a goal) and intuitively associated with the absence of selfhood and thus with not being an agent. (b) Even someone tied up can cause mental states in themselves or others. But anything that can't cause a mental, or cognitive, state at least in itself is not intuitively an agent. So it seems that wanting and being able to cause are intimately associated with being an intelligent agent, and thus every agent must want at least one state and be able to cause at least one state as Axiom 1 requires.
Copyright © 2008 by Ian Williams Goddard. All rights reserved.