Noesis The Journal of the Mega Society Issue #189     December 2009

Special Issue
Astronomy and Space (Part One)

Contents

About the Mega Society/Copyright Notice		2
Editorial	Kevin Langdon	3
Can Appropriate Use of Laser-Induced   Breakdown Spectroscopy Get to the Bottom of   Long-Term Martian Surface Mysteries?	Andrew Beckwith	4
Report on Two Talks at the Triple Nine Society’s   GGG999 Conference, September 2009	Kevin Langdon	6
The Earths of Alpha Centauri	Michael Edward McNeil	8
Thermalizing Background Radiation	R. Fred Vaughan	21

About the Mega Society

The Mega Society was founded by Dr. Ronald K. Hoeflin in 1982. The 606 Society (6 in 10⁶), founded by Christopher Harding, was incorporated into the new society and those with IQ scores on the Langdon Adult Intelligence Test (LAIT) of 173 or more were also invited to join. (The LAIT qualifying score was subsequently raised to 175; official scoring of the LAIT terminated at the end of 1993, after the test was compromised). A number of different tests were accepted by 606 and during the first few years of Mega’s existence. Later, the LAIT and Dr. Hoeflin’s Mega Test became the sole official entrance tests, by vote of the membership. Later, Dr. Hoeflin’s Titan Test was added. (The Mega was also compromised, so scores after 1994 are currently not accepted; the Mega and Titan cutoff is now 43—but either the LAIT cutoff or the cutoff on Dr. Hoeflin’s tests will need to be changed, as they are not equivalent.)

Mega publishes this irregularly-timed journal. The society also has a (low-traffic) members-only e-mail list. Mega members, please contact the Editor to be added to the list.

For more background on Mega, please refer to Darryl Miyaguchi’s “A Short (and Bloody) History of the High-IQ Societies”—

http://www.eskimo.com/~miyaguch/history.html

—the Editor’s High-IQ Societies page—

http://www.polymath-systems.com/intel/hiqsocs/index.html

—and the official Mega Society page,

https://www.megasociety.org/

Noesis, the journal of the Mega Society, #189, December 2009.

Noesis is the journal of the Mega Society, an organization whose members are selected by means of high-range intelligence tests. Jeff Ward, 13155 Wimberly Square #284, San Diego, CA 92128, is Administrator of the Mega Society. Inquiries regarding membership should be directed to him at the address above or:

ward-jeff@san.rr.com

 Opinions expressed in these pages are those of individuals, not of Noesis or the Mega Society.

Copyright © 2009 by the Mega Society. All rights reserved. Copyright for each individual contribution is retained by the author unless otherwise indicated.

Editorial

Kevin Langdon

These are exciting times in astronomy. There’ve been important new findings which have altered our understanding in almost every area of the field, from planetology to cosmology.

· As Dr. Andrew Beckwith points out in his article in this issue, new evidence has substantially increased the likelihood of life on Mars.

· Over 400 planets have been found orbiting other stars. Almost all of these planets are very large, similar to the planets of the outer solar system (and, in some cases, considerably larger). Using a telescope with a field of view of 105 square degrees (two orders of magnitude larger than ordinary astronomical telescopes), the Kepler space telescope, launched in March 2009, is designed to detect earth-sized and smaller planets. This will give us a much more complete picture of planetary systems.

· The mysteries of dark matter attraction and dark energy repulsion have only deepened with new discoveries and new models. No consensus has yet emerged.

Noesis is publishing two special issues on astronomy and space. This is the first such issue. The second will be published in February 2010. The field of astronomy has always attracted many highly competent amateurs. This special issue on astronomy and space continues that tradition. It has attracted several fine submissions. I expect it to stimulate much thought. Your feedback and submissions for our second astronomy and space issue are solicited. This first issue contains::

· a short article by Andrew Beckwith on the potential use of laser-induced  breakdown spectroscopy for exploring the Martian surface.

· a report by the Editor on two talks at the Triple Nine Society’s GGG999 Conference on the Labor Day weekend, “Blowing Bubbles in Space,” by Heather Preston, and “The Little Satellite That Could,” by Derek Buzasi.
For more on the conference see: http://www.ggg999.org .

· “The Earths of Alpha Centauri,” by Michael McNeil, discussing the pos-sibility of earthlike planets around Alpha Centauri A and/or B.

· “Thermalizing Background Radiation,” by R. Fred Vaughan, a thought-provoking alternative to the standard cosmological model.

.The deadline for Noesis #190 is February 15, 2010. Material for this issue is needed. Submissions by both members and nonmembers of the Mega Society will be considered.

Cover photo: Planetary Nebula K-55 (NASA, Hubble Space Telescope)

Can appropriate use of laser-induced breakdown spectroscopy get to the bottom of long term Martian surface mysteries?

Andrew Beckwith

 Introduction

Laser-induced breakdown spectroscopy (LIBS) uses a high-power pulsed laser, focused on the target, to provide more than a megawatt of power on a small spot less than a milli-meter in diameter for a few billionths of a second. The potential this has for supplying hard data confirms that LIBS is capable of determining differences in rock types from a stand-off distance of 5.4 meters. Such a test was performed by Roger Wiens, Justin Thompson, James Barefield, David Vaniman, Sam Clegg, and colleague Horton Newsom (Institute of Meteoritics at the University of New Mexico) in a lab in Los Alamos where  the LIBS technique was tested on two Martian meteorites and a terrestrial analog rock.

Where LIBS can be used

This sort of technology has been deemed appropriate for the next generation of Mars rovers, perhaps as soon as 2011 to 2012. Among other things, appropriate testing of this type may allow us to determine whether or not volcanism or meteorite impacts—and not standing water—could be responsible for the sulfate sediments detected on Mars by NASA’s Opportunity rover, according to two separate studies.

Volcanic vents and/or  Ejecta clouds?

1.  The Ejecta clouds theory proposed by Paul Knauth of Arizona State University in Tempe is a meteorite-impact-driven phenomenon, making use of the thin Martian atmosphere for dispersal of material blasted above the Martian surface by surface bombardment by meteors.
2. Volcanic venting supposes that water steam and sulfur dioxide spewed from the vents would have formed sulfuric acid, which would have reacted with the vol-canic ash to produce sulfate salts. This for now seems to be the hands-on favorite of planetologists, with many espousing variants of this idea.

Answering the question of whether or not bacteria
could have lived on the Martian surface at some time

Another appropriate use of the LIBS technique may be to determine whether or not life existed in prior eras on Mars. Note that a new study of a meteorite that originated from Mars has revealed a series of microscopic tunnels that are similar in size, shape and dis-tribution to tracks left on Earth rocks by feeding bacteria

The problem is, though, that just because there is an analogy between certain terrestrial structures suggesting life and those which appear in Martian rocks, the case for such structures confirming present or former life on Mars is not ironclad. As noted by Martin Fisk, a professor of marine geology in the College of Oceanic and Atmospheric Sciences at Oregon State University:

Virtually all of the tunnel marks on Earth rocks that we have examined were the result of bacterial invasion. In every instance, we’ve been able to extract DNA from these Earth rocks, but we have not yet been able to do that with the Martian samples.

The LIBS technique in itself may not be the game changer in deciding this last question, but it would be perhaps the next best thing to having Martian soil scooped up and sent back to Earth to start to get additional information on this question. And, of course, there are practical difficulties, to put it mildly, in transporting Martian boulders/rocks from the Martian surface back to Earth labs, which the LIBS technique, if appropriately used, may help us avoid

Conclusion: LIBS is a step in the right direction

Considering the enormous logistical difficulties in having human beings travel to Mars, make scientific measurements, and return to Earth, the LIBS technology may be the best we can do for the foreseeable future in unraveling the many bizarre and complex issues surrounding Martian planetary science.

Reference

Thompson, J. R., R. C. Wiens, J. E. Barefield, D. T. Vaniman, H. E. Newsom, and S. M. Clegg (2006), “Remote Laser-Induced Breakdown Spectroscopy Analyses of Dar al Gani 476 and Zagami Martian Meteorites.” Journal of Geophysical Research, v. 111, doi: 1029/2005JE002578.

Report on two talks at the Triple Nine Society’s
GGG999 Conference, September 2009

Kevin Langdon

Heather Preston - Blowing Bubbles in Space: The Birth and Death of Practically Everything (Astronomical)

http://www.mensafoundation.org//Sites/foundation/NavigationMenu/Programs/Conversations/RevolutionsinCosmology/RevCosmology.htm

Heather Preston is a mission scientist for several NASA missions, including the Spitzer Space Telescope, Wide-Field Infrared Explorer (WIRE), and the Kepler mission searching for terrestrial-class planets around other stars. She taught physics at the U.S. Air Force Academy and is an instructor in two distance education programs. She was an Operations Astronomer for the Hubble Space Telescope for five years and has published over 50 scientific papers, specializing in asteroseismology, gas dynamics, and computational fluid dynamics.

Heather began with some basic astronomical facts. She said that the normal-matter part of the universe is 90% hydrogen, >9% helium, and <1% everything else, and that all heavy elements come from supernovae. That is, since most of the universe is gas, it’s no shock that many of the extended structures we see are due to gas-dynamic processes, but it is a bit surprising that a huge number of these extended phenomena are bubbles of one kind or another. And then she added that, in addition to supernovae, stars, planetary nebulae, and galaxies with active nuclei all blow bubbles. She showed some stunning astronomical photographs to illustrate this point.

She spoke about the dynamics of different kinds of objects and the mechanisms through which they blow off the material that creates the characteristic bubble shape. Starting at the low-energy, early-life end, while many protostars are surrounded by gaseous clouds which coalesce into spinning, flattened disks in the process that can lead to planet formation, they’re hard to observe in visible light because there’s too much obscuring dust. However, they can be imaged in considerable detail in the infrared; and in the infrared there is outflow from the star, frequently constrained at the “waist” by the disk—resulting in an hourglass-shaped “double bubble.”

Almost all stars will pass through a “red giant” phase of their lives, and at the end of that phase they will lose some mass to the interstellar medium (the ISM is the ultra-low-density “atmosphere” of the galaxy—random gas drifting around that generally would make a good laboratory vacuum on Earth). Stars less than a couple of times the mass of the Sun will wind up with a fast wind emitting a significant amount of gas (the outer layers of the star) to drop the central star’s mass to below 1.4 solar masses (white dwarf limit), and that mass-loss period results in a bubble in space called a “planetary nebula.” The becoming-exposed core of the central star is a white-hot and small pre-white-dwarf, giving off ultraviolet radiation that ionizes and excites the puffed-off outer layers of the star, so that they glow. Different scenarios for the star (whether it’s a binary, how much mass is lost, at what times) will result in different shapes for the nebula. Heather showed many breathtaking images of these varied “bubbles” from the Hubble, Spitzer, and Subaru missions.

Supernovae are relatively rare events. There is one in a large galaxy like the Milky Way about once every 50 years. Typically only stars which end their red-giant phase with more (sometimes much more!) than twice the mass of the sun explode as supernovae and expel really high-speed shells of gas. Those shells typically glow for thousands of years, heated to excitation by the shocks set up when high-speed extremely hot low-density gas ploughs into the lower-speed and much cooler ISM. The result: big bubbles—splashy young ones or delicate arcs of old ones.

Finally, the truly cosmic-scale gas bubbles we see are the result of outflows from active galactic nuclei. Our own Milky Way has a super-massive black hole at its center (an SMBH has millions of solar masses, and is composed of millions of stars that are close enough together that they become a singularity—the higher the mass of a black hole, the lower the initial matter density that is required to create one). The nuclei of other galaxies typically are inhabited by SMBH’s, also, and are much farther away. But it has recently become possible to obtain images that have made it possible to study the “bubbles” blown by gas outflows from these active galactic nuclei. The shapes of the flows are determined by factors such as how much gas is “feeding” the central black hole, whether the disk is fatter or thinner, etc. The field of Computational Fluid Dynamics gives us the tools to work backward from the picturesque and intriguing shapes of these gas bubbles to the physical conditions producing them—because the same set of fluid-dynamic principles underlies all of these phenomena.

Derek Buzasi - The Little Satellite That Could

http://www.nytimes.com/1999/08/24/science/an-astronomical-bonanza-from-a-washed-out-satellite.html

(a New York Times article on Dr. Buzasi and the subject of this talk)

Derek Buzasi is Professor of Astronomy at the U.S. Air Force Academy in Colorado Springs, currently on active duty for the US Navy. He is an Affiliate Professor at the Department of Astronomy, University of Washington, and is a member of the science team for the Kepler mission, mentioned above under the talk by his wife, Heather Preston.

How do we know anything about the internal structure of the sun? Starting in the 1960s, Robert Leighton developed a Doppler-based observing technique which detects oscillatory motions on the Sun with amplitudes of hundreds of meters per second. These motions are due to acoustic waves traveling inside the Sun. The study of these waves is called helioseismology, and the study of starquakes in general is called asteroseismology.

The sun, like other stars, resonates in about a million different modes simultaneously. Although convective “noise” generates a wide range of frequencies, since the star can be considered as a resonant cavity only a finite number of these waves interfere construc-tively and survive. Each mode that survives tells us something about the structure of the star. Since long-wavelength waves penetrate deeper into the sun, while shorter wave-lengths sample only the surface, using all of them we can construct a model of the entire stellar interior. From such models, we can learn about details of internal rotation, convection, and structure.

The Wide-Field Infrared Explorer (WIRE), launched in 1999, was a NASA satellite intended to make a four-month infrared survey of the entire sky, specifically focusing on starburst galaxies and luminous protogalaxies. Unfortunately, the main scientific instrument on this satellite failed shortly after launch. It was considered a total loss but Dr. Buzasi realized that the onboard star tracker, a small guide scope on the side of the main scientific instrument, could be repurposed for asteroseismology studies. This approach resulted in interesting results within two weeks and eventually became the primary instrument for the mission over the next 7 years. WIRE data typically achieved precision twenty to a hundred times better than ground-based asteroseismology studies. The best data have a relative precision level of approximately one part per million. Dr. Buzasi showed examples of observational data and its uses in testing stellar models.

The Earths of Alpha Centauri

Michael Edward McNeil

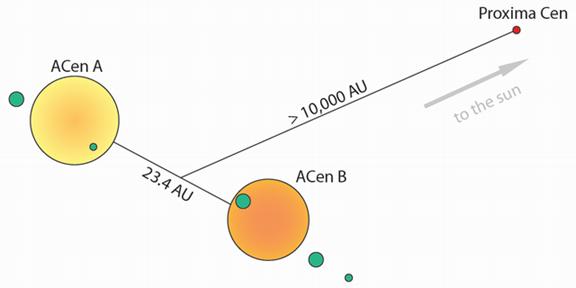
Figure 1.  Schema of the Alpha Centauri system

University of California at Santa Cruz astronomy and astrophysics graduate student Javiera Guedes (first author), together with her coauthors, have published a fascinating piece in The Astrophysical Journal titled the “Formation and Detection of Terrestrial Planets around α [Alpha] Centauri B” ¹ which in my view deserves far wider audience and consideration than it can receive in that journal, however prestigious and renowned a scientific journal it assuredly is.

The subject of that paper, the binary Alpha Centauri star system (also known as Rigil Kentaurus or Toliman), at some 4.4 light years (or about 1.3 parsecs) distant from the Sun, is the closest extrasolar stellar system to our own Solar System and Earth.  The brightest star in that system, Alpha Centauri A, is quite similar to our Sun in mass (at ~1.105 solar masses), and extremely similar in  color and thus temperature (classed, like the Sun, as a spectral type G2 V, a so-called “yellow dwarf”), whilst its companion Alpha Centauri B is only slightly smaller (~0.934 times the Sun’s mass) and a bit redder and therefore cooler (spectral type K1 V) than the Sun.  One might note that the Alpha Centauri system (at about 5.6-5.9 Gyr) is between 1 and 1.3 billion years older than our Sun and Solar System, while it’s about half again as rich in “metals” (as astronomers regard them: i.e., elements heavier than hydrogen and helium) as our own system.

Though it has a third, much smaller (~0.1 solar mass) spectral type M “red dwarf” com-panion star known as Proxima Centauri—swinging at an enormous distance (perhaps a fifth of a light year) away from its principals—Alpha Centauri is essentially a close binary star system; and thus one might imagine that the gravitational influence of Alpha Centauri’s two principal stars, A and B, on each other would forestall prospects for any stable planets circling either star.  As it happens, however, those primary components of Alpha Centauri are not actually all that close, orbiting each other some 23 astronomical units (23 times the distance between the Earth and the Sun, abbreviated AU) apart from each other—equivalent to B (or A) circling between the orbits of Uranus and Neptune (in our Solar System) with regard to the other—and as a result planets orbiting beyond what would be the orbit of Mars here, up to some 3 AU away from its primary (or well into our asteroid belt) are not ruled out around either star; moreover any planets (if they exist) are computed with high probability to be stable for the requisite billions of years time.  Moreover, planets have already been discovered orbiting other roughly similar binary stars (e.g., γ [Gamma] Cephei, HD 41004, and Gliese 86) having basically equivalent separations from each other.

Indeed, Alpha Centauri A and B would probably even have performed a positive perturbative role with regard to each other’s incipient planetary systems, similar to that which the gas giants Jupiter, Saturn, and beyond are thought to have played in planetary evolution here in our Solar System, to wit providing “perturbations allow[ing] for the accretion of a large number of planetary embryos into a final configuration containing 3-4 bodies.”  (Note that we omit end-note references in all quotes from The Astrophysical Journal article.)

Alpha Centauri B, as a cooler, “quieter,” less variable and flare-prone star than Alpha Centauri A (or the Sun for that matter), as a result is somewhat easier than A to detect any planets circling round.  Thus it is on B that the authors concentrate their attention, estimating that after only about three years of “high cadence” observations (watching B on basically every night that there’s good seeing and the telescope is available), one could detect (using the so-called Doppler or radial-shift detection method) a planet of only some 1.8 Earth-masses circling within B’s so-called “habitable zone,” while somewhat smaller worlds ought to become apparent in only a couple of years more.

Whilst it’s also sometimes possible to detect extrasolar planets by observing their transit (or eclipse) across the disk of their primary star as seen from Earth, that method requires that the plane of any planets’ orbits be closely aligned with the direction of our Sun with respect to that system—which is obviously extremely unlikely when attempting to locate worlds circling any particular star—and thus such an approach is suitable only for statistical surveys of a great many stars, not for finding the planets of any specific suns.

In addition to evaluating how Alpha Centaurian planets could be observed from the perspective of Earth, the authors conducted a number of computed simulations (eight in all) of possible routes to planetary system formation, starting from initial circumstances “mimic[ing] conditions at the onset of the chaotic growth phase of terrestrial planet formation in which collisions of isolated embryos, protoplanets of approximately lunar mass, dominate the evolution of the disk.  During this phase, gravitational interactions among planetary embryos serve to form the final planetary system around the star and clear out the remaining material in the disk.  At the start of this phase, several hundred protoplanets were presumed to orbit the star [in] nearly circular orbits.”  Each run of the simulation “populate[d] the disk with N = 400 to N = 900 embryos of lunar mass […].”

Simulation number 7 (see Figure 3), specially exemplified herein and in The Astrophys-ical Journal article (known as r600_1 there), started with 600 embryos.

All bodies in the simulations interact only through gravity, and the evolution of their positions and velocities with time were calculated using the MERCURY code, designed for the presence of a binary companion and allowing planetary embryos to collide and stick together to form larger planets.

The investigators “focus[ed] on terrestrial planet formation around α Cen B[…].” As they note, “[P]lanet formation around α Cen A is expected to be qualitatively similar.”

Figure 2 illustrates how simulations of the evolution of a planetary system surrounding Alpha Centauri B typically progressed (using simulation 7).

The authors describe the figure thusly:

Figure [2] shows the late evolutionary stage of a protoplanetary disk initially containing 600 moon-mass embryos [appearing in Figure 3 as simulation number 7].  The radius of each circle is proportional to the radius of the object.  Bodies in the outer parts of the disk ([orbital semimajor axis] a > 3 AU) are immediately launched into highly eccentric orbits and either migrate inward to be accreted by inner bodies, collide with the central star, or are ejected from the system […].  In this simulation, ~65% of the total initial mass is cleared within the first 70 Myr.  By the end of simulation [7], four planets have formed.  One planet has approximately the mass of Mercury and is located at a = 0.2 AU, two 0.6 [Earth mass] planets form at a = 0.7 and a = 1.8 AU, and a 1.8 [Earth mass] planet forms at a = 1.09 AU.

[…]  All of our simulations result in the formation of 1-4 planets with semimajor axes in the range 0.7 < a < 1.9 AU […].  We find that 42% of all planets formed with masses in the range 1-2 [Earth masses] reside in the star’s habitable zone [Fig. 3], taken to be 0.5 < a_hab < 0.9 [AU].  […]  All of our disks form systems with one or two planets in the 1-2 [Earth] mass range.

Figure 3 illustrates the results of all eight Alpha Centauri B system evolution simulations that the authors performed.  The especially illustrated simulation used herein appears as number seven near the bottom, whilst for comparison our Solar System is shown to scale at top.

We see that realistic astrophysical simulations predict that planets surrounding Alpha Centauri B (as well as a similar system circling A) are quite likely. What will it take to actually find such worlds, if they do exist?

As noted earlier, due to the extreme unlikelihood of any specific stellar planetary system’s equivalent of our “plane of the ecliptic” (the plane in which its planets’ orbits

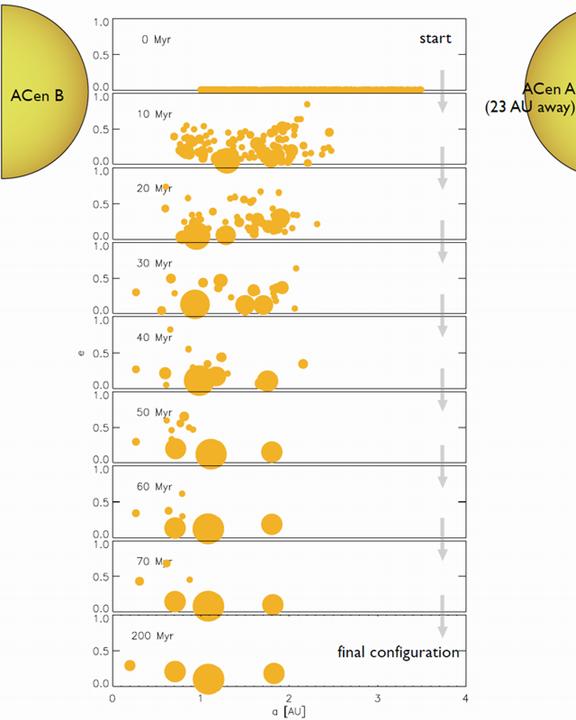
Figure 2.  Simulated evolution of a planetary system (simulation 7) for Alpha Centauri B

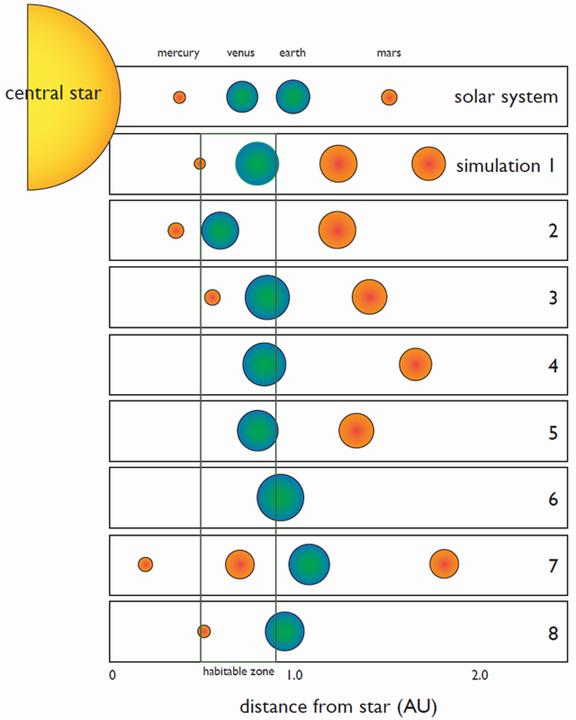
Figure 3.  Simulated planetary systems of Alpha Centauri B

generally circle) exactly lining up on edge as seen from Earth, the transit method for detecting extrasolar planets cannot be applied (other than by the remotest chance) for locating worlds orbiting specific suns—leaving only the “Doppler wobble” method available for finding planets in more particular circumstances.  Even for that approach
to work, the plane of a given star’s planetary orbits must not directly face the Sun (i.e., the axis of that plane mustn’t be oriented directly toward or away from the Sun), as there has to be some planetary radial velocity toward or away from the Earth for us to detect.  Inasmuch as theoretical considerations imply that the orbital plane of planets circling either star of a close binary system should in general be aligned with the orbits of the stars themselves as they revolve about each other—and since in the case of the Alpha Centauri system, its two stars’ orbital plane can be observed to be inclined to the line of view from here in the Sol System by a mere 11 degrees (the axis of that plane being almost perpendicular to the line of sight from the Earth)—planets circling either A or B are nearly ideal for detection from Earth using the radial-velocity technique.

Indeed, as the authors of this study conclude:  “α Cen B is overwhelmingly the best star in the sky for which one can contemplate mounting a high-cadence [nightly] search” for extant terrestrial worlds, among other things because “α Cen B is exceptionally quiet, both in terms of acoustic p-mode oscillations and chromospheric activity.”

They note that “[t]he radial velocity [Doppler] detection of Earth-mass planets near the habitable zones of solar-type stars requires cm s⁻¹ [centimeter per second velocity] precision,” whereas Alpha Centauri A exhibits (rather Sun-like) oscillatory noise on the order of 1 to 3 m s⁻¹ (meters per second), which would effectively swamp attempts to detect planets circling A using near-term technology.  Alpha Centauri B, on the other hand, as a fundamentally quieter star, displays peak amplitude noise on the order of 0.08 m s⁻¹ (8 cm/second), which is also far higher in frequency than the periods of any potential terrestrial planets to be detected.  As a result, a “focused high cadence approach involving year-round, all-night observations would effectively average out the star’s p-mode oscillations.”

Observations also reveal that Alpha Centauri B exhibits much less chromospheric variability associated with stellar flares than does A (the former modifying its x-ray brightness only within a factor of two over a couple of years time whilst A could be observably seen to vary by an order-of-magnitude factor of ten).

The paper further points out that:

α Cen B is remarkably similar in age, mass, and spectral type to HD 69830, the nearby K0 dwarf known to host three Neptune-mass planets.  Both α Cen B and HD 69830 are slightly less massive than the Sun with masses 0.91 and 0.86 [solar masses] respectively.  Their estimated ages are 5.6-5.9 Gyr for α Cen B and 4-10 Gyr for HD 69830.  Both stars are slightly cooler than the Sun:  α Cen B is a K1 V with [an effective temperature] T_eff = 5350 K, while HD 69830 is a type K0 V star with T_eff = 5385 K.  The stars have also similar visual absolute magnitudes, M_V = 5.8 for α Cen B and M_V = 5.7 for HD 69830; however, due to its proximity to us, the former star appears much brighter (m_V = +1.34), allowing for exposures that are ~60 times shorter.  One can thus use a far smaller aperture telescope, or alternatively, entertain a far higher observational cadence.

Moreover, Alpha Centauri A and B being so close to each other in space as well as physically similar to one another allows parallel observations of the two stars to reveal concurrent variations which, seen in both, allow identification of systematic artifacts in the observational process that can thus be filtered out of any meaningful results.  Furthermore, as the study notes, the position of Alpha Centauri at about -60° declination in our southern sky is nearly perfect for virtually continuous night-by-night observations from two existing vantage points, the Las Campañas Observatory together with the Cerro Tololo Inter-American Observatory, both in Chile, either of which ought to provide up to almost 300 viewing days a year (60 days a year being basically unavailable while Alpha Centauri annually passes behind the Sun, plus a few more days lost as a result of bad weather).

Inasmuch as the proportionate density of binary, roughly-solar-mass component star systems in this part of the galaxy is only about 0.02 per cubic parsec (1 cubic parsec = ~35 cubic light years), and at this time the Alpha Centauri system hovers a mere 1.33 parsecs away from us, we’re very lucky here in the Solar System having α Cen proceeding so close nearby during this era for us to perform this highly desirable search.

As The Astrophysical Journal paper concludes:  “All these criteria make α Cen B the ideal host and candidate for the detection of a planetary system that contains one or more terrestrial planets.”  Indeed, “our current understanding of the process of terrestrial planet formation strongly suggests that both principal components of the α Cen system should have terrestrial planets.”

Given that extremely tantalizing possibility, what will it take to find those worlds orbiting Alpha Centauri B, if they exist?  As the authors note:

A successful detection of terrestrial planets orbiting α Cen B can be made within a few years and with the modest investment of resources required to mount a dedicated radial-velocity campaign with a 1 m class telescope and high-resolution spectrograph.  The plan requires three things to go right.  First, the terrestrial planets need to have formed, and they need to have maintained dynamical stability over the past 5 Gyr.  Second, the radial velocity technique needs to be pushed (via unprecedentedly high cadence) to a degree where planets inducing radial velocity half-amplitudes of order cm s⁻¹ [centimeter per second] can be discerned.  Third, the parent star must have a negligible degree of red noise [in] the ultralow frequency range occupied by the terrestrial planets.

In this paper, we have made the case that conditions 1 and 2 are highly likely to have been met.  In our view, the intrinsic noise spectrum of α Centauri B is likely all that stands between the present day and the imminent detection of extremely nearby, poten-tially habitable planets.  Because whole-Sun measurements of the solar noise are intrin-sically difficult to obtain, our best opportunity to measure microvariability in radial velocities is to do the α Cen AB Doppler experiment.  The intrinsic luminosity of the stars, their sky location, and their close pairing will allow for a definitive test of the limits

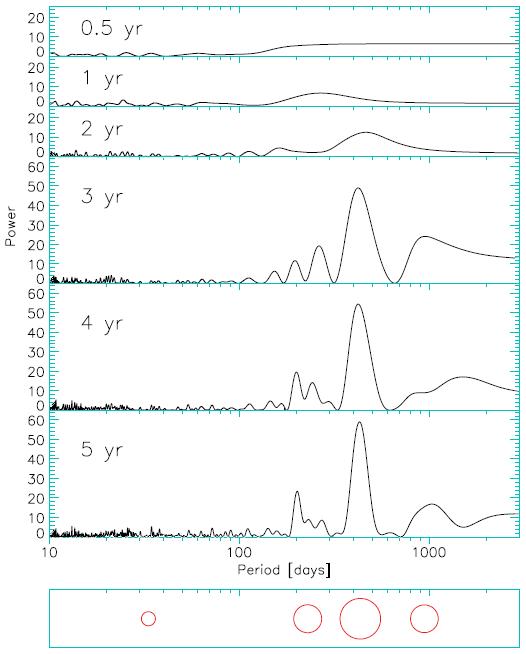
Figure 4.  How the detection “periodogram” for a simulated Alpha Centauri B planetary system (simulation 7) evolves over 5 years of observations

of the radial velocity technique.  If these limits can be pushed down to the cm s⁻¹ level, then the prize, and the implications, may be very great indeed.

At this point over four hundred planets have been discovered circling other stars beyond the Sun—all thus far found, due to hitherto operative technical limitations, necessarily being much larger than Earth and thus far from being really terrestrial in type.  The Alpha

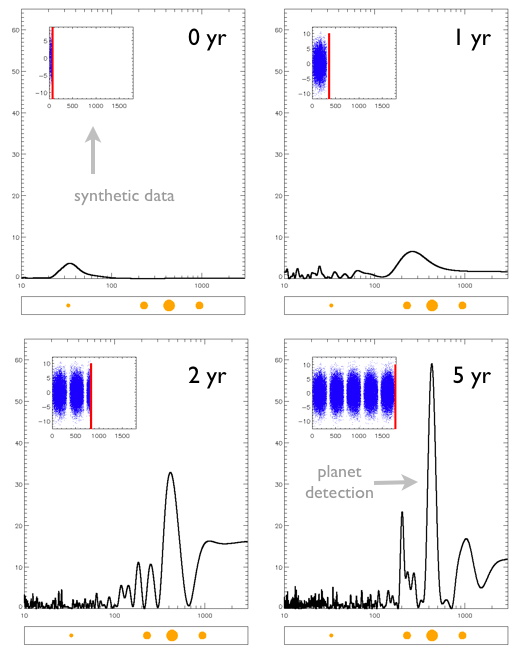
Figure 5.  How nightly observations over 5 years build that periodogram for a simulated Alpha Centauri B planetary system

Centauri system offers the opportunity to refine those limits downward toward worlds much closer in size, and thus potentially in habitability, to the Earth.

Figures 4 and 5 illustrate how such a high-cadence search over a period of several years could zero in closer and closer toward identifying any planets of Alpha Centauri B that are truly terrestrial in scale.

As the capability for detecting truly terrestrial-type planets circling round nearby stars approaches, we’re on the cusp of an adventure grander by far than Columbus’s voyages to the New World or other great discoveries of the age of exploration, not only for its tremendous scientific value (finding what variety of worlds so-called “terrestrial” planets can form, not to speak of the enormous significance of possibly discovering other inde-pendently evolved organisms inhabiting them), but also for the sake of the future history of mankind, along with the ultimate fate of all life dwelling on—but presently restricted to this single egg-basket of—our planet Earth.

In a discussion such as this of potential planets circling the component stars of the Alpha Centauri system, special recognition is due the late biochemist and most prolific science fiction and fact writer Isaac Asimov, for it was he who, just a half-century ago (in June, 1959), penned his far-sighted essay “The Planet of the Double Sun” ² concerning the possibility of just such worlds existing.  A quarter-century later, in 1985, he wrote another essay on the subject of life near Alpha Centauri called “The Double Star” ³; whilst in 1976 Asimov published an entire book on Alpha Centauri, The Nearest Star. ⁴

In regard to the intrinsic value of such planets, it’s worth noting the ending of Asimov’s affecting science fiction novel The End of Eternity ⁵, which serves as the introduction to his famous Galactic Empire and Foundation series of stories.  In the context of this tale, when it is realized that ready access to the universe is at hand for humanity (provided they take a critical step, namely make a certain change to the past), the principal protag-onist wonders aloud what good it would really do if they should indeed accomplish it:

“And what would have been gained?” asked Harlan doggedly.  “Would we be happier?”

Whereupon his erstwhile enemy, more recent ally, and soon to be spouse replies:

“Whom do you mean by ‘we’?  Man would not be a world but a million worlds, a billion worlds.  We would have the infinite in our grasp.  Each world would have its own stretch of the Centuries, each its own values, a chance to seek happiness after ways of its own in an environment of its own.  There are many happinesses, many goods, infinite variety. . . .  That is the Basic State of mankind.”

Now, on the cusp of the fortieth anniversary of mankind’s (as representative of all life on Earth) first visit in all the billions of years’ history of Earthly life to another planet, it’s time to get on with it.  Let’s find those worlds!

Glossary

absolute magnitude	intrinsic visual brightness of an object as it would be seen from a fixed distance—in the case of a star this is established as being 10 parsecs or 32.6 light years away
AU	astronomical unit, abbreviated AU (sometimes symbolized ua): one AU is the average distance between Earth and the Sun—about 150 million km or 93 million miles
binary star system	star system consisting of two stars orbiting each other about a common center of mass
chromosphere	relatively thin (perhaps 2,000 km thick in the case of the Sun) semitransparent layer in a star which lies just above its opaque photosphere or visible “surface”
chromospheric variability	activity or variability in a star which occurs within its chromo-sphere
Doppler wobble	method for locating extrasolar planets by the radial velocity (as seen from Earth) perturbations they induce in the motions of the primary star they orbit
Earth mass	mass of the Earth: some 6 × 10^24 kg or about 0.31% the mass of Jupiter
dynamical stability	long-term probabilistic stability of planets over gigayears time against perturbations that would eject them from the system, or throw them into their primary star or each other
eccentric orbit	an orbital path that is a highly flattened ellipse rather than being approximately circular
ecliptic	rough plane in which the planets of the Solar System (exception: Pluto) generally orbit
extrasolar body	planet, star, or other body which orbits or moves outside the realm of the Solar System
gas-giant planet	giant planet like Jupiter which is composed principally of the gases hydrogen and helium
Gyr	gigayears: billions of years
habitable zone	region surrounding a star where temperatures on an Earth-type planet circling within that zone are suitable for life as we know it—in our Solar System it is considered to lie between about 0.95 to 1.37 AU from the Sun
half-amplitude	absolute (positive) value of maximum amplitude, as opposed to amplitudes varying in sign between positive and negative over a continuous approximately sine-wave cycle
high cadence	astronomical observations conducted at a high frequency—e.g., nightly—in order to sample the orbit of a planet thoroughly and to reduce the noise.
Jupiter mass	mass of Jupiter: around 2 × 10^27 kg, or about 0.1% the mass of the Sun or 318 times the mass of Earth
light year	the distance that light travels in vacuum in a year: about 9 trillion km or 6 trillion miles
MERCURY (code)	software package designed to solve for the positions and velocities of planetesimals in the gravitational field of a host star. The program is publicly available and was written by John Chambers.
Mercury mass	mass of the planet Mercury: about 3 × 10^23 kg or around 5.5% the mass of Earth
metals	metals as astronomers regard them: to wit, elements heavier than hydrogen and helium
microvariability	small amplitude variability
Moon (or lunar) mass	mass of the Moon: some 7 × 10^22 kg or about 1.2% the mass of Earth
Neptune mass	mass of Neptune: close to 1 × 10^26 kg, or some 17 times the mass of Earth or 5.4% of Jupiter’s mass
p-mode oscillations (or pressure-mode oscillations)	p-mode oscillations are acoustic wave propagations driven by internal pressure fluctuations within a star.  They are acoustic in nature because they depend on the local sound speed of the star’s interior. The fluctuations are periodic and therefore the waves are a source of noise for radial-velocity based planet searches.
parsec	the distance at which an extrasolar body’s parallax with regard to Earth’s orbit around the Sun subtends an angle of one second of arc—approximately 3.26 light years
periodogram	measured periodic radial velocity variations in a star over time that might indicate the presence of planets
photosphere	opaque layer of a star which constitutes its visible “surface”
protoplanet	Moon-sized or larger planetary embryos orbiting a star within its protoplanetary disk
protoplanetary disk	rotating disk of gas and dust surrounding a fledgling star which may accrete into planets
radial velocity	velocity component of an extrasolar star or planet directed toward or away from Earth
red noise	low-frequency random noise emitted by a star under observation
semimajor axis	one-half of the length of the long axis of an elliptical orbit— equivalent to a body’s average distance from its primary
spectral type	classification system for stars based on a star’s color and thus its surface temperature
spectrograph	instrument measuring an object’s light output across a spectrum of optical frequencies
stellar flare	eruption of plasma from the surface of a star
Sun (or solar) mass	mass of the Sun: about 2 × 10^30 kg or some 333,000 times the mass of Earth
terrestrial planet	planets consisting primarily of rocks (normally silicate rocks) at least near the surface; as opposed to gas-giant planets
transit method	method for detecting an extrasolar planet by observing the dip in its primary star’s light output as the planet passes directly in front of the star’s disk as viewed from Earth

Acknowledgments and References

Many thanks to talented astronomy and astrophysics graduate student Javiera Guedes (and first author on the Astrophysical Journal paper) for her support and suggestions as well as permission to use the figures from her and her co-authors’ article, and supplying her own version of Figure 5, and to Barbara Fasulo, who assisted Ms. Guedes with the illustrations. Ms. Guedes has already personally conducted observations of Alpha Cen-tauri at Cerro Tololo Inter-American Observatory and is to do more in 2010 and 2011.  Observations are currently being conducted by Professor Debra Fisher (Yale) and her team.  Kudos to all the investigators in this study, and best wishes in the great search!

¹ J. M. Guedes, E. J. Rivera, E. Davis, and G. Laughlin (all at the University of California at Santa Cruz, Astronomy and Astrophysics department), E. V. Quintana (SETI Institute, Mountain View, CA), and D. A. Fischer (San Francisco State University, Physics and Astronomy department), “Formation and Detection of Terrestrial Planets around α Centauri B,” The Astrophysical Journal, Vol. 679, Issue No. 2 (2008), pp. 1581-1587; doi: 10.1086/587799.

² Isaac Asimov, “The Planet of the Double Sun,” The Magazine of Fantasy and Science Fiction, June, 1959, Mercury Press, New York.  Collected in Fact and Fancy, Doubleday & Co., Garden City, NY, 1962; also in Asimov on Astronomy, Anchor Press, Garden City, NY, 1975.

³ Isaac Asimov, “The Double Star,” American Way, American Airlines, September 3, 1985.  Collected in The Dangers of Intelligence And Other Science Essays, Houghton Mifflin, Boston, 1986.

⁴ Isaac Asimov, Alpha Centauri, The Nearest Star, Lothrop, Lee & Shepard Co., New York, 1976.

⁵ Isaac Asimov, The End of Eternity, Doubleday & Co., Garden City, NY, 1955, p. 187.

Thermalizing Background Radiation

R. Fred Vaughan

fred@vaughan.cc

Any theory of the cosmos must account for apparent equilibrium conditions as-sociated with the microwave background radiation.  There is in addition a light element percentage issue, most notably the universal hydrogen-to-helium ratio.  It is an interesting fact that the energy that would have been released primarily as gamma radiation in pro-ducing the notable 24% helium by mass from a primordial hydrogenous plasma observed throughout our universe is precisely the energy density found in the microwave back-ground radiation.  Of course gamma ray production from this source would be incon-sequential in comparison to what would have been produced by the annihilation of a billion or so universes as massive as what we observe.  Those are the alternatives.  The unfathomable catastrophe is what standard cosmological model proponents argue as the preferred accounting for what is observed.  This position derives, of course, from the observed cosmological redshifting and inferred consequences of that phenomenon.  Nonetheless, the aforementioned cosmological coincidence is definitely among the more significant phenomena to be accounted for by models that attempt to explain the cosmos.

Whatever the ultimate origin of the radiation that now clutters the universe as 2.725 K blackbody radiation, unless it were to have resulted as the mere emanation of a ‘soup’ of material particles at that temperature, there is a requirement that the original radiation that was its penultimate cause be ‘thermalized’ to reach equilibrium.  That process involves the intercourse of radiation and matter.  The scattering of radiation by which this is effected involves both diffraction and absorption followed by re-emission, but in any case can only be effected by the interaction of electromagnetic photons with material particles.  In contradistinction to the means of reaching equilibrium of particulate energies, which achieve that result by mere collisions one with another, radiation cannot redistribute its photon energies (except for very exceptional situations that do not alter the points being made here) other than by their interactions with matter.

Normally, by which term one usually means ‘here on planet earth’, radiation tem-perature and the kinetic temperature of associated material particles in a thermal medium in equilibrium would be identical in any system characterized by blackbody radiation.  However, what seems ‘normal’ for the thermodynamics studied in laboratories has not involved virtually infinite ‘cavities’ where redshifting of radiation takes place, as is perti-nent to cosmology.  In standard cosmological models it is assumed that background radiation had continuously been in equilibrium with a dense plasma that expanded adia-batically until, at a redshift of about 1,250, the plasma is thought to have become so cool and diffuse that it no longer supported scattering.  That point in spacetime after which radiation is no longer considered to have interacted with matter is termed the ‘surface of last scattering’.  These two phases in the preparation of the background radiation have necessarily to be handled differently in the standard cosmological model.

Perhaps there is a less conflated explanation.

Understanding Blackbody Radiation

Before proceeding it is important that the reader understand what ‘blackbody’ radiation is.  It is sometimes called ‘cavity’ radiation as we did above because it is the distribution of photons that would be observed emanating from a tiny opening in a cavity that is in thermal equilibrium.  In Figure 1 such a cavity is illustrated that is maintained at a constant temperature by having been placed in a ‘heat bath’ long enough for the cavity wall to have reached a stable thermal equilibrium temperature.  Experimental analyses of blackbody radiation are performed using just such apparatuses.

For obvious reasons what would be seen if one were to look into the hole of such a contraption is called “blackbody radiation.”  The detected radiation has an invariable form named “Planck radiation distribution” because, in contrast to the notorious failure of its predecessor the “Rayleigh-Jeans distribution,” Planck was able to precisely match what is observed.  This “blackbody” spectrum has the functional form r[ l, T] dl that is illustrated graphically in Figure 2.  Its formula is given by:

r[ l, T] dl = (2p h c / l⁵ ) ( e K / l T -1 )^-1 dl                                                           Eq. 1

This particular parametrical representation is denominated, ‘spectral radiant exitance’ and is expressed per unit wavelength l.  The units of r[ l, T] are ergs / cm² sec.  The constant factor K in the exponent is defined as:

K º h c / k @ 1.441 cm K,

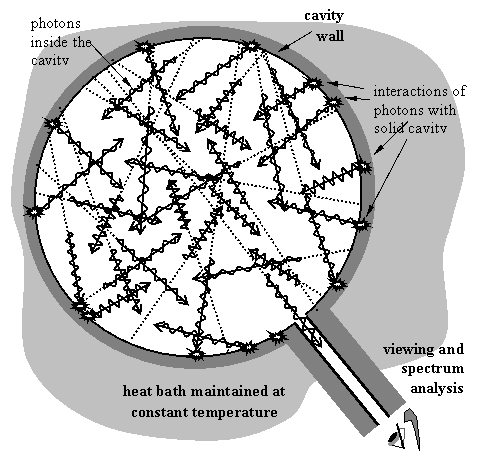
Figure 1:  Apparatus for observing ‘cavity’ radiation

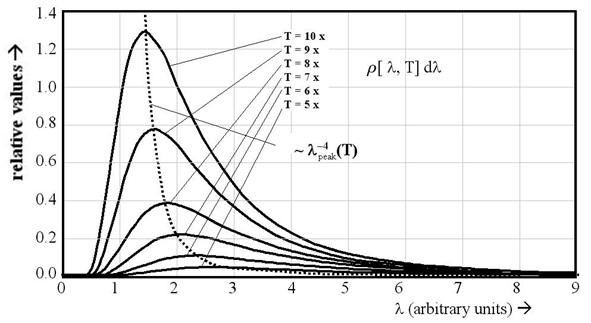
Figure 2:  Blackbody spectrum and its fourth order relationship to temperature

where the individual factors in this definition are:  Planck’s constant h = 6.63 x 10^-27 erg seconds, the speed of light in vacuum c =  2.998 x 10¹⁰ centimeters per second, and Boltz-mann’s constant k = 1.3807 x 10^-16 erg per degree K, are all given here in the cgs system of units.  The wavelength associated with the peak of this distribution function is:

l_peak = 0.2 ( h c / k T ) @ 0.2898 / T cm

Assigning a value of T = 3 x 10⁸ K would, for example, result in a peak radiation wave-length of l_p » 10^-9 cm in the ‘hard X-ray’ portion of the electromagnetic spectrum.

The quantum energy of a single photon as a function of its wavelength l is:

E_p[l] = h c / l ergs

Thus, dividing the wavelength distribution function r[l,T]dl by the speed of light determines the energy per cubic centimeter in the wavelength interval l to l + dl.  If we integrate this function over all wavelengths, we obtain the following energy density for a ‘blackbody’ distribution:

E[T]  = ( 8 p⁵ k⁴ / 15 h³ c³ ) T ⁴ @ 7.5 x 10^-15 T ⁴ ergs / cm³                                               Eq. 2

The total energy radiated in one second through a square centimeter of surface area, I[T] by such a blackbody involving any substance in thermal equilibrium is given by Stefan’s empirical formula:

I[T]  º c E[T]   = s e  T ⁴ erg / cm² sec

Here s = 2.268 x 10^-4 erg / cm^-2 K^-4 is the Stefan-Boltzmann constant and e is the emissivity, i.e., the efficiency of emission relative to that of a theoretically perfect black-body.  (Note that emissivity and absorptivity are equal for a given substance.) 

In Figure 3 we have depicted the situation in which the ‘heat bath’ of Figure 1 is produced by an ideal gas of indefinite extent for which there would be no fringe effects.  The temperature of the gas is maintained at the required value of the cavity wall.  In an equilibrium situation characterized by the conservation of energy, total energy will be partitioned equally among all constituents of a gas.  This includes not only particulate components of the gas, but also the thermalized photons of electromagnetic energy.

Figure 3:  ‘Cavity’ embedded in an ideal gas at a fixed temperature

In this figure, as in Figure 1 above, all photons are seen to have originated as emissions or reflections off the wall of the cavity, and are assumed to remain unchanged during transmission unless and until they interact with the cavity wall in a subsequent scattering event.  However, for a ‘bath’ comprised of the stationary state ideal gas shown in Figure 3, the situation is similar to taking away the cavity wall altogether and allowing the gas to move freely throughout what was formerly the cavity as is now shown in Fig-ure 4.  Photons would then scatter off of particles in the gas rather than the wall of the cavity, but to similar effect.  However, in order that it indeed be to similar effect, the gas must be dense enough or its extent great enough that the same density of photons is real-ized within the conceptual cavity walls as shown.

In his quantum theory of radiation Einstein derived the Planck distribution from first principles using the Boltzmann energy distribution of particles in an ideal gas rather than as mere oscillators in a cavity wall.  In Figure 4 we show the same photons shown in the previous figures within the now only ‘conceptual cavity’ radius although recognizing that similar photons will exist throughout the gas.  Some of the depicted photons will now have originated outside the spherical region where the cavity had been situated.  Inter-actions all involve a material particle that could be considered a part of a contorted ‘surface’ area, however, each at a different distance from any central point.  Importantly, the observed distribution of photons within the former cavity region will be essentially the same whether there is a solid, fixed cavity wall or not.

Figure 4:  Radiation situation in an ideal gas

Thermal equilibrium will pertain to regions that are at least several times the ‘optical thickness’ interior to any surface boundary at which there is a temperature gradi-ent.  This condition ensures that radiation and material particles will be in thermodynamic equilibrium throughout this interior region.  The ‘optical thickness’ is a distance that radi-ation must penetrate in a medium before its intensity is reduced to e^-1 @ 0.368 of its original value.  This involves radiation energy being converted into mechanical energy in the medium via absorption from scattering.  In such cases, where the equipartition of energy typically demands all constituents of a thermal medium share a common kinetic temperature, the associated radiation is not excluded.

Other than for thermonuclear reactions, the redistribution of energy in material substances does not alter the number of entities among which the energy will be shared.  This is not the case for electromagnetic energy, however.  The number of photons at each wavelength and the total number of photons in the distribution will be altered by the thermalization process.  It is also significant that the density of material particles does not enter Planck’s formula at all.  The reason is that although ‘heat’ is currently perceived as tantamount to the movement of constituent particles, the blackbody form of distribution assumes an enclosed cavity as shown in Figures 1 and 3, and to the same effect in figure 4.  If the conceptual cavity wall shown in Figure 4 had been less than several times the optical thickness of the medium from the boundary of the substance, then the blackbody form might not have been realized if there were lower temperatures out away from the cavity wall.  The reason for this is that some of the photons in the ‘mix’ could have been generated by an interaction with a particle of lower temperature at a large distance from the conceptual cavity wall.  There would still be ‘thermal’ radiation given off, but it would not have achieved the blackbody form of the equilibrium situation and the equi-partition of energy could not be rigorously applied.  In this way the density of particles does provide a constraint on the thermalization process.

So far we have only discussed situations in which there is no redshifting of the involved radiation.  Redshifting will become an issue in situations in which the optical depth is appreciable relative to distances for which an observable redshift occurs.  As in the previous situation we will see that for ‘thin’ (i.e., diffuse, low density) substances the average temperature of the contorted cavity surface in Figure 4 to which any blackbody radiation distribution would apply may be significantly lower than the kinetic temper-ature of the particles, even at equilibrium.

Figures 1 and 4 illustrate two of the ways in which electromagnetic radiation can achieve and maintain a blackbody spectrum, either by interacting with solid surfaces at a fixed temperature or by interacting with particles in an optically thick gaseous substance that is in equilibrium at the given temperature.  These interchanges in both cases bring about the complete sharing of energy characterized by the phrase ‘equipartition of en-ergy’.  In each of the three figures above it is the individual exchanges of energy with particulate entities that produce the redistribution of electromagnetic energy as the system proceeds toward equilibrium, so that ordinarily these two instances would be very sim-ilar.  Thus it is that these two illustrated situations are not ordinarily considered to be different in any very essential way.

However, although the two situations illustrated in Figures 1 and 4 may not be considered as being different, they very definitely are.  When photons in an ideal gas ex-perience redshifting a subtle but major difference is introduced.  The difference involves the concentric spheres of propagation distance, indicated by dashed circles in Figure 4, not requiring the same amount of time for a photon to cover the distance from its last interaction to its next one in the two cases.  So that if redshifting is occurring in one case during the interval of a photon’s transit, it will arrive at its next interaction with a dif-ferent wavelength (and associated energy) in that situation.  The different interaction history of the photons, even those within the symbolically indicated confines of the cavity domain (or any cubic centimeter of the space) will alter the resulting distribution in ways that need to be investigated.  This is very similar to how any change in the medium tem-perature that might occur over the duration of the longest propagation time would affect the distribution.  The question we will be addressing is: “What would be the resulting distribution of photons in such cases?”  The answer to this question is extremely relevant to cosmology.

Blackbody Radiation in a redshifting environment

The mechanism responsible for redshifting has a significant impact on the results of the thermalization process.  If, as standard-model cosmologists suggest, space expands ‘beneath’ the photons as they travel (particularly in the second phase of the background radiation production process), the mechanism is straightforward.  Propagation from a ‘surface of last scattering’ to current observations of the microwave background merely involves a Doppler redshift associated with a receding wall at a higher temperature.  In the standard model it is assumed that there has been no scattering of background radiation propagated from a redshift of about 1200 where (when) it is assumed that the earlier plasma had cooled sufficiently to coalesce into neutral atomic and molecular substances.  This assumes that intergalactic space is, for all practical purposes, a complete vacuum, and although this seems somewhat reasonable on the face of it, it isn’t.  Proponents be-lieve the universe to have been so ‘smooth’ that the ‘last scattering’ would have happened at almost exactly the same redshift (instant in the past) in all directions, with radiation scattered off the last extant plasma continuing to propagate to the present observations without incident.  They argue that it is as though there were a radiating ‘solid’ surface at about 3,400 K at that distance/redshift.

The effect of redshift (defined here as Z) on radiation is to lengthen the wave-length of all propagating radiation as follows:

Z º ( l_o - l_e) / l_e                                                                                                            Eq. 3

Here l_o is the observed wavelength of the radiation and l_e is the initially emitted wavelength of that same radiation.  This is reflected in the statement,

l_o = ( Z  + 1) l_e

Substituting this expression into Eq. 1, we obtain:

r[ ( Z  + 1) l_e, T ] dl = ( r[ l_e, T ] / ( Z  + 1)⁴ ) dl

Similarly also from Eq. 1 we have that:

r[ l, T_e / ( Z  + 1) ] dl = ( r[ l, T_e ] / ( Z  + 1)⁴ ) dl

A fourth order temperature dependence was similarly apparent in the functionality of the blackbody intensity in Eq. 2 above.  There it is apparent that a blackbody that is at a temperature twice the number of degrees Kelvin as another will radiate at sixteen times the intensity, as was shown in Figure 2 above.  Clearly, we have the relationship:

r[ l, T_o] dl = r[ l, T_e] ( T_o/ T_e )⁴ dl

This was illustrated in Figure 2.  From this and the previous equations it is apparent that:

T_o⁴  = T_e ⁴ / ( Z  + 1)⁴

Employing assumptions of the standard cosmological model with regard to a surface of last scattering, since the observed blackbody temperature in our universe is T_o = 2.725 K, we have for the temperature of that surface:

T_e = 2.725 ( Z  + 1)

So if Z = 1,250, we would have that T_e » 3,400 K.  So the microwave background radi-ation temperature is not so much of a prediction as a retrofitting of two numbers that combine to give a third, which is observed.  Nor is it obvious that either of the inferred numbers is precisely correct.  Other combinations would have worked.

Figure 5 shows the relative abundance of various neutral and ionized forms of hydrogen and helium as functions of kinetic temperature, each shown for one (solid line) and ten (dotted line) dynes of dynamic pressure, with considerably lower pressures obvi-ously reducing condensation temperatures commensurably further.  Certainly the as-sumed density profile of the standard model plays into the assignment of a value for Z.    However, there is a significant issue raised by this figure; it is that there would be a non-negligible range of transition temperatures, densities, and redshifts between states of fully ionized plasma and neutral atomic and molecular matter.  It seems reasonable from the figure that there would be a transition phase of on the order of a thousand degrees with corresponding differences in pressure, with the redshift changing by several hundred.  Throughout that interval plasma scattering would be taking place to varying degrees.  This certainly makes the tiny variation in the observed background of one part in ten to the fourth or fifth seem an unlikely consequence of this ‘de-coupling’ situation.

A 3,400 K plasma assumed as the effective ‘cavity wall’ would have been respon-sible for 10 ergs per cubic centimeter radiated throughout all space—a tremendous energy density.  In comparison, the microwave background involves about 4 x 10^-13 ergs cm^-3.  Suppose that, instead of a cavity wall at only the one redshift, portions of that high temperature wall had been distributed throughout all space with radiation from the more distant segments of the contorted wall redshifted more than that from closer ones.  Suppose further, as we did above, that radiation originating at each such ‘surface’ seg-ment would not be involved in subsequent scattering.  In this case the resulting energy density E'[T] would be the integral of the energy density over all the surfaces as follows:

¥

_o

E'[T] = _ò E[T] / ( Z  + 1)⁴ dZ = (1/3) E[T]

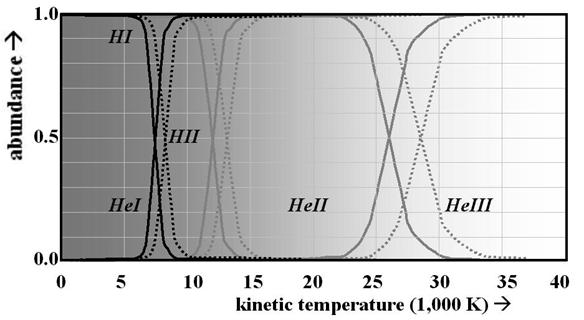
Figure 5:  Light element ionization properties

So the inferred temperature of the observed radiation distribution would be less than that of the kinetic temperature of a unified cavity wall but only by the factor of (1/3)^1/4 @ 0.76, i.e., 10¹⁴ or 10¹⁵ times greater than what is observed.  But that is just the implications of energy density, not to be construed as implying a blackbody distribution of radiation.  This is more of an inverted Olbers’ Paradox reductio ad absurdum argument.  You can see why advocates of the standard model hold to the ‘one-wall’ explanation as they have.

Next let us look at the explanation of the earlier phase of background radiation production according to the standard model.  In this case rather than no scattering, with the universe expanding ‘beneath’ the radiation, there is thought to have been a homo-geneous plasma with continuous scattering such that at each instant the radiation would have been in instant equilibrium with particulate matter in the plasma state.  The situation is characterized as an adiabatic expansion in which the ensemble of photons and charged particles all share a common temperature.  There is a major difference in how these two phases must be analyzed.  In this case rather than merely invoking a simplified Doppler redshift, we have no redshift assumed during the propagation of thermal radiation, with each succeeding snapshot pieced together, with redshift having occurred in the cracks.  Thermodynamics with varying temperature and pressure are not specifically addressed.  The explanation is oversimplified to assume that thermalization will have caught up with expansion at each instant and that redshift can be treated as a fixed commodity at each instant.  But it can’t be; there would necessarily be a lookback continuum of redshifts of observable radiation at each instant.

It is necessary to incorporate the fact that in addition to radiation being scattered from particles characterized by a given temperature and pressure, that inevitably there would be redshifted photons in the mix that have been scattered off of more distant particles.  This radiation from more distant regions would appear to have been scattered off of ‘surfaces’ at different temperatures and that would require re-thermalization.  This problem does not seem to have ever been addressed by proponents of the standard model with regard to this earlier phase of the thermalization process.  At a minimum it would have to be shown that the plasma at each instant was sufficiently dense in each era that a single temperature and redshift could characterize associated radiation.  Alternatively it might be argued that the effects of redshift would have precisely compensated for de-creasing temperatures and densities.  However, the required argument, whatever it turns out to be, has been waived.  But an explanation of some kind is definitely required.

Blackbody effects in an alternative cosmological model

In the preceding discussion there was little discussion of the particular mechanism of redshifting.  Although in the early phase explanation of background radiation of the standard cosmological model, it would have been hotter and the concentric circles in Figure 4 would have gotten closer together due to the greater density in the past.  That would not be without analytical consequence to the predictions.  But that is a deficit for apologists to acknowledge and address as they see fit.

In a scattering model proposed by the author the nature of equilibrium conditions in a redshifting medium is of paramount significance.  In this model, developed in detail in his book, Cosmological Effects of Scattering in the Intergalactic Medium (ISBN:  978-0-578-02625-1), the author describes how relativistic effects of forward scattering in a hot plasma for which relativistic effects cannot be ignored produces a redshift.  To produce an equivalent effect to what is attributed to cosmological redshift via the Hubble constant, the average product of the density and temperature of the plasma must be on the order of 4.15 x 10³ K cm^-3.  The Hubble constant is H_o = 7.14 x 10^-29 cm^-1; this is about 70 km sec^-1 Mpc^-1 in the more common units used in deference to the Doppler interpretation of the standard cosmological model.  The scattering model also assesses the absorption due to scattering in the intergalactic medium and finds a broadband absorption that results in a diminution of luminous flux by a factor of (Z+1)^-1.  The effect of this is precisely equivalent the factor attributed to time dilation of photon emissions in the Doppler interpretation of redshift.  So results are very nearly equivalent to those of the ‘concor-dant’ version of the standard model but without the requirement for “acceleration” when redshift gets much beyond unity.

But we are discussing thermalization here.  When one does solve the problem of thermalization in a redshifting medium that was introduced above, one discovers that the temperature of the radiation and the uniform average kinetic temperature of material particles from which scattering is effected may differ significantly one from the other.  It is a demonstrated fact that the microwave background radiation is at 2.725 K.  It seems manifestly obvious, no matter how loud the chatter of standard model apologists, that the rest of the universe is considerably hotter than that.

The energy density of this background radiation is 4.13 x 10^-13 ergs per cubic centimeter.  That energy had to have come from somewhere, and it is the nature of ther-mal equilibrium that whatever the source of energy in a closed system, it will eventually redistribute itself to a common energy density.  At the outset we mentioned that the density of matter for which a 24%-by-mass conversion to helium from a hydrogenous plasma would produce the appropriate radiation energy density is 5.49 x 10^-31 grams per cubic centimeter.  That value is tightly snuggled between the best estimates of the univer-sal baryonic density.  So it is hardly a stretch to conclude that the background radiation may well have originated in the nucleosynthesis of helium rather than the destruction of a billion universes like our own.

Behold, gamma ray bursts!  What these bursts may signify is that perhaps there is some ongoing stationary-state resurgence of matter that had gone down the neutron-star/black-hole sinks, and like supernovas, only more so, it has erupted, producing a flux of primeval particles including a glut of neutrons to maintain that ratio.  The profiles of radiation from gamma ray bursts observed to as far as we have seen into the universe produce conditions that mimic those for which nucleosynthesis of helium is argued to have occurred following a big bang.  Suppose that the upheaval of black holes that have seemed to merely be the sinks of baryonic matter is possible.  And why wouldn’t that be possible if the alternative eruption of an entire universe out of a much more gigantic black hole is conceived as possible?  Then we have the makings of a “Steady State” universe without requiring creation ex nihilo, as required by an expansion; that is the legitimate reductio ad absurdum argument against the standard cosmological model as well.

Smithsonian Astrophysical Observatory

At the observed baryonic mass density of the universe, the equilibrium kinetic temperature determined using the author’s redshifted blackbody analysis would be about 2.8 x 10³ K.  This is a realistic assessment of the average temperature of the bulk of the material universe that is observed all around us in planets, dust, stars and galaxies.  But these values are too low for the redshifting mechanism that the author has hypothesized in his ‘tired light’ accounting for the Hubble constant.  However, it is in the rich cores of galaxy clusters that the much higher average value of the product of temperature and den-sity is achieved.  Here observed temperatures are as high as 10⁹ K and densities as high as 10^-3 gm cm^-3, producing the extreme redshift extended streaks in redshift surveys denomi-nated “the fingers of god.”  Refer to Figure 6 taken from the CFA redshift survey, in particular at azimuthal angles 16h and 13h as well as elsewhere throughout the plot.

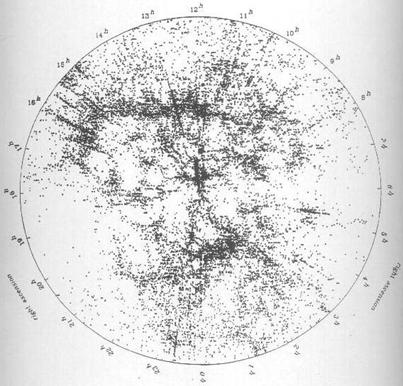
Figure 6:  CFA redshift survey data showing the ‘fingers of god’

These “fingers” are a major rationale for dark matter in the universe.  If the velo-city dispersion associated with a Doppler interpretation of these redshift streaks is attrib-uted to the dynamics of the mass of the galaxy cluster itself, it require up to seven times the mass as that observed from the luminosity of the involved galaxies to hold the gravi-tational system together. That and somewhat similar arguments involving rotation curves for individual galaxies are what ‘dark matter’ is all about.  Clearly, according to the au-thor’s scattering model, there is no such thing.  There is no need for such a concept.

The separation of cluster cores on any line of sight is as much as ten to a hundred Mpc, i.e., more than 10²⁶ to 10²⁷ cm, so that the cosmological redshift is an average of a-whole-lot-of-a-little and a-little-of-a-whole-lot.  This produces the lumpiness that also characterizes redshift surveys where slices are superimposed on each other with regard to waves of galaxy intensity at approximately 100 Mpc intervals.  See Figure 7 taken from the SDDS redshift survey for declinations between zero and six degrees.  The same basic phenomena are observed at all declinations well above the obscurations of the Milky Way.  Thus, the scattering model provides mutually consistent parameter values that col-lectively account for cosmological features.

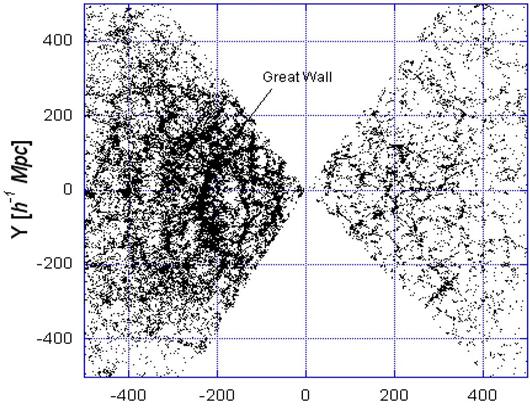
X [h-1 Mpc] à

Figure 7:  Density ripples in the SDSS redshift survey from 0 < Dec < 6

Predictions of the author’s scattering model rely exclusively on traditional phys-ics.  The model is, therefore, conservative in its approach to accounting for cosmological redshift, redshift dependence of luminosity data, comoving number densities, microwave background radiation, light element abundances, and other phenomena.  It allows for the time required for the observed structures in the universe to have developed, and does not invoke unknown physical concepts such as inflation theories to fit vaguely anticipated deductions of a supposed early universe.  Nor does this scattering model require that the universe be comprised of predominately mysterious forms of exotic matter or obscurely defined ‘energy’ to account for observations in our current universe.  It does not bemoan ‘missing matter’.  It seems hardly coincidental that the characteristics of the intergalactic plasma should so precisely account for such extremely diverse observations for which the standard models have required alternative inconsistent parameter values and hitherto unknown types of matter and physical concepts for their accounting.  However, that is the case.

Summary of the implications of thermalization in a redshifting medium

Since the effects of scattering discussed in this paper assume an equilibrium situ-ation of the universe at large, the theory does not accommodate evolutionary effects in the universe as a whole, although the observed galaxy and galaxy cluster level developments are certainly to be expected.  The standard models have not excelled in accounting for apparent evolutionary effects, but such developments are at least compatible with the standard cosmological model.  There are a number of observations that have suggested to many researchers that their explanations require evolutionary effects, and these must obviously be accounted for otherwise by the scattering model.  Not least of the cited phenomena are the microwave background radiation, comoving number densities of galaxies, the ‘blueness’ of some types of distant galaxies, light element abundance per-centages, Lyman-a forest data, etc..  Therefore, it has been necessary for the author to provide at least cursory alternative explanations of these diverse phenomena in order for his approach to be taken seriously.  These resolutions have followed as natural concom-itants of the scattering model.

The author has operated always in the spirit of Peebles’ suggestion that was quoted as an introduction to chapter 1 with regard to it being “sensible and prudent that people should continue to think about alternatives to the standard model, because evidence is not all that abundant.” He is convinced that his scattering model has excelled in this endeavor.

Having addressed many, although by no means all, of these peripherally related phenomena, the author finds his results most gratifying.  The microwave background radiation formerly considered to have been the exclusive claim of standard models has been shown to result from an indefinitely extended universe in the state in which we observe it today.  There is actually much better agreement than previously accounted for by standard models inasmuch as the resolution ties in other pertinent data considered irrelevant by the standard model.  The explanation is actually much more complete, hav-ing relied on a more thorough analysis of blackbody equilibrium conditions applicable to a redshifting medium, which would actually refute some of the claims made for the standard model scenario.

The implied values of temperature and density to account for redshift have been shown to also be completely compatible with observed background radiation as well as with the observed variability of mass densities with redshift.   It brings into account the uniform X-ray background emanating from galaxy cluster cores.  Light element thermo-nuclear production is also in complete accord with the approach taken here.  But there is also an attractive hypothesis involving the range of parameter values observed in gamma ray bursts that suggests a recycling of compressed data from black holes that seem to ‘bounce’ back into this universe rather than into an alternative one as some proponents of multiverse metaphysics have intoned.  Ultimately it will be observation that will be the arbiter.

The scattering model provides more convincing explanations for a wide range of heretofore-unexplained phenomena.  Naturally, it has no problems with the ‘too early ap-pearance of galaxies’; the distribution of galaxies fits a uniform pattern once former relativistic radial redshift assumptions have been backed out of the data.  It eliminates quandaries of recent observations by the Hubble space telescope that indicate that the ages of certain stars within our own galaxy based on their metalicity may actually exceed the age of the universe predicted by many standard model versions using parameter values required to match other observations.  It resolves dilemmas that have given rise to mysterious ‘dark matter’ and ‘vacuum energies’ without necessitating these exigencies.

Importantly, the velocity dispersion of the galaxies, particularly in rich clusters, is readily accounted for as resulting from combinations of the denser plasma medium producing a more rapid redshifting through the clusters than by presuming mysterious forms of matter.  This merely involves the same redshifting mechanism that is responsible for cosmological redshift.  Rotational anomalies of individual galaxies are explained now in similar terms of increased plasma densities of spherical ‘halos’ interior to and extend-ing into remote regions on the spiral arms and beyond.   These halos seem to extend be-yond individual galaxies, merging into the extremely hot intracluster gases and has thereby suggested to some researchers that the inferred ‘dark matter’ is virtually all asso-ciated with such extended halos (Bahcall, 1999).  The observed temperatures and den-sities of this plasma gas produce a redshift rate well in excess of Ho across the extent of these clusters that mimics the attributed ‘velocity scatter’.

Appeal to establishment to perform extended analyses

Analytical results reported here have been produced by the use of a couple of analytical approaches that the author believes never to have been used before.  He feels that it is important that these same analyses be applied with regard to other cosmological models to determine the legitimacy of prediction claims that have been made.  Previous research has been remiss in assuming there would be no effects without performing the appropriate analytical computations in situations where the impact has been shown to be major for any and all cosmological theories.  Basically there are three such areas that have supported the author’s investigations:

1.   Absorption effects applicable to the dispersion associated with the propagation of electromagnetic radiation through a plasma.

Absorption is the immediate consequence of light transmission through any scattering medium.  In both the standard model and the scattering model the Lyman-a forests provide examples for which analyses are required and have been performed to determine implicit absorption effects of the column density of neutral hydrogen be-tween astronomical objects and their observation.  However, there is also a significant plasma component present in the intergalactic regions through which we observe the distant cosmos, and the absorption effects of a plasma differ considerably from those of neutral substances.

These effects must be analyzed, and have been for the author’s scattering model.  Significantly, however, it is even more essential to the standard cosmological model because in that conjecture there is a much more dense plasma hypothesized to have been present over the majority of the time period since the big bang as well as a unique transition hypothesis for which analyses must be performed.

Whether this absorption is characterized as broadband, as is the case for the scat-tering model, or absorption with unique wavelength functionality depends upon the absorption coefficient value determined for the medium as well as the redshift func-tionality appropriate to the theory.  But in any case, the analysis must be performed to determine the amount of luminosity loss that must be attributed to this absorption process.

In the standard models there is a luminosity diminution factor attributed to time dilation whose functionality is precisely that of a broadband absorption like that which has been determined to apply to the scattering model.  But if time dilation is claimed as the cause of this reduction in luminosity in the standard model, an asso-ciated assertion must be made, and confirmed, that at no phase of the scenario would there be any observable plasma absorption.  That in the propagation of electromag-netic radiation though billions of light years of intergalactic space none would be absorbed seems unlikely.  In any case, that is another conjecture that needs to be ad-dressed.

2.   A convergent diffraction effect associated with forward scattering processes through a plasma medium.

Forward scattering is involved in the imaging of objects viewed through any inter-mediate medium.  In our atmosphere at sea level photons are replaced by virtually identical forward-scattered photons at sub-centimeter intervals for light transmission at sea level.  Other than quite unrelated noncoherent scattering and absorption pro-cesses, this does not affect our ability to see ‘objects’ per se out to distances beyond the optical depth of the medium that is determined by these processes.  This phe-nomenon of forward scattering is certainly pertinent to cosmological observations and their interpretations.

Obviously forward scattering typically involves nothing other than mundane opti-cal physics, to little effect.  However, the intergalactic medium is hardly typical of media that have been studied in the laboratory.  In addition, those who have been the most significant contributors to forward scattering theory have specifically excluded media for which relativistic velocities of charged particles are involved.  Thus, the well-known wavelength invariance that applies to this process is not applicable to such media without investigation.  With regard to the intergalactic medium, that investigation is essential.

The author has performed such an investigation and found that the relativistic aberration and transverse Doppler effects collaborate to effect a diffraction for which conservation of energy and momentum imply a lengthening of wavelength at each ‘extinction’ in the forward scattering process.  However, the analyses also show that the aberration of the diffraction angle does not preclude forward scattering.  In effect, its only impact is to lengthen wavelength, which when combined with the wavelength dependence of extinction intervals, produces Doppler-like redshifts.

This physical phenomenon is not unique to the author’s scattering model; it is a physical effect associated with forward scattering in a plasma generally.  Its effects can be observed in the redshifting that occurs in the chromosphere at the limb of the sun.  Therefore, this effect must apply to the standard model as well.  At a minimum this must impact the ‘dark matter’ controversy applicable to domains for which plas-ma densities and temperatures are appreciable.  The effects of forward scattering through that medium must be addressed.

3.   The effect of redshift occurring throughout a scattering medium on the thermalization process.

It seems singularly amazing to the author that no one seems to have ever even considered the most immediate impact of redshift on the equilibrium conditions es-sential to blackbody radiation.  But that does indeed seem to be the case.

Of course standard model advocates have addressed the redshift impact sim-plistically as appropriate to two separate phases identified in that model.  The first involves plasma scattering for which the unstated assumption is that the plasma is dense enough that there is no redshift occurring between scattering events.  The second applies Wein’s law to an assumed receding cavity wall associated with ‘de-coupling’.  That is essentially the depth of the redshift-related analyses that have been performed to ‘predict’ the eventual state of background radiation.  But, of course that is not pre-diction, it is a post-diction.  The associated redshift of that ‘wall’ of last scattering as the determining factor is retrofitted to the observation.  There is a stark contrast between the oversimplification of that characterization and the complexity of the actual problem.  Also, there is a gross avoidance of the coincidence of the energy produced by the nucleosynthesis of helium from a hydrogenous plasma to establish the universal ratio that corresponds so precisely to the amount observed in microwave background radiation.

In the scattering model for which the universe is assumed to be in an essentially stationary state, there is definitely redshifting that takes place between diffuse plasma scattering events.  Thermalization involves all the absorption, re-emission, and non-coherent scattering so that essentially all the objects we see are included in the mix.  When one takes these facts into account in a redshifting environment, the kinetic temperature of the matter with which the radiation is thermalized by scattering is no longer constrained to a value directly linked to blackbody radiation as in the adiabatic expansion phase assumed by the standard model.  Nor is that constraint valid once the impact of intermediate redshifting is included in the scope of analyses.

So it is manifestly clear that cosmological model advocates who do not take these factors into account do not adequately address the implications of the models they propound.